



![]()


Si la notion de relativité est l'oeuvre de Galilée, c'est bien Copernic qui en est le précurseur. Il est le premier à déloger la Terre de sa place centrale dans l'univers pour la ramener au rang d'une planète comme les autres en rotation autour du Soleil. Copernic est donc le premier à suggérer que la Terre est en mouvement et ouvre ainsi la voie à la "relativité Galiléenne".
|
|
Nicolas Copernic (1473-1543) chanoine polonais, publiera en 1543 "De revolutionibus orbium caelestium", oeuvre qui présente pour la première fois depuis Aristarque de Samos la Terre comme tournant autour du Soleil, provoquant ainsi l'effrondrement du système de Ptolémée en vigueur depuis presque 1500 ans ! Encore ensorcellé par les sphères Platonicienne, son modèle d'univers présentait les planètes comme décrivant des cercles autour du Soleil et n'était guère plus précis que le modèle de Ptolémée sous bien des aspects. Il faudra en définitive attendre l'année 1621 pour que Kepler, après des années de recherche et plus de 900 pages de calculs acharnés, montre enfin que les trajectoires des planètes sont en réalité des ellipses dont l'un des foyer est occupé par le Soleil. |
Quoi de plus immobile que ne l'est apparemment la Terre ? Aucune sensation, aucune expérience nous prouve qu'elle se déplace à raison de 30 km/s par rapport au Soleil et ce n'est donc pas un hasard si toutes les théories élaborées depuis Platon présentaient la Terre comme une sphère immobile au centre de l'univers. Pour rendre compte avec précision du mouvement des différentes planètes sur la voute céleste, les modèles se compliquèrent peu à peu..On vit ainsi apparaître progressivement les notions "d'épicycles" et de "déférents" (Eudoxe, Aristote, Ptolémée) mais personne, pas même Tycho Brahé, n'osa vraiment déloger la Terre de sa place privilégiée lui conférant ainsi du "mouvement".
Galillée est surement le premier à vraiment comprendre qu'il est physiquement impossible de faire une différence entre repos et mouvement (de translation uniforme) même si cette notion de relativité du mouvement avait déjà été mise en relief par Aristote lui même. Il s'agissait chez le philosophe grec (384 av JC - 322 av JC) de souligner plutôt la difficulté qu'il pouvait y avoir à découvrir le "vrai mouvement" mais dont l'existence n'était pas réellement mise en cause. Galilée va plus loin et affirme que la notion de mouvement absolu est vide de sens; "Le mouvement est comme rien !", il est de la nature même du mouvement de n'être que relatif. Aucune expérience ne permet de savoir si un corps est en mouvement ou en repos, seul le mouvement d'un corps par rapport à un autre possède un sens.
Citons cette extrait du livre "Dialogue sur les deux principaux systèmes du monde" publié en 1632 par Galilée et visant à convaincre ses lecteurs de l'impossibilité de détecter le mouvement:
" Enfermez-vous avec quelques amis dans une vaste salle, bien à couvert, au fond d'un grand navire; munissez-vous de mouches, de papillons et d'autres petits animaux volants; prenez un grand vase d'eau et mettez-y des poissons, suspendez au plafond un petit seau dont l'eau tombe goutte à goutte dans un autre vase à col étroit posé sur le sol: le navire restant immobile, observez soigneusement comme les petits animaux volettent avec des vitesses égales dans toutes les directions de la salle; les poissons nageant indifféremment de tous les côtés; les gouttelettes tombant toutes dans le vase posé par terre; et vous-même lançant quelque chose à un ami, n'aurez pas besoin de lancer avec plus de force dans une direction que dans une autre, pour des distances égales dans tous les sens....Mettez maintenant le navire en marche, aussi vite que vous voudrez. Alors, pourvu que le mouvement soit uniforme, et non oscillant de-ci, de-là, vous ne discernerez pas le moindre changement dans les effets décrits et aucun d'entre eux ne pourra nous indiquer si le navire ets en mouvement ou arrêté; la cause de la permanance de tous ces effets est que le mouvement est commun au navire et à tout ce qu'il contient, y compris l'air....posons donc comme principe de notre investigation que, quel que soit le mouvement que l'on attribue à la Terre, il est nécessaire que, pour nous qui sommes les habitants d'icelle et par conséquent participants de celui-là, il reste parfaitement imperceptible et comme n'étant pas..."
|
Galilei Galiléo (1564-1642) : Il construit en 1609 une lunette astronomique avec laquelle il observe les cratères et montagnes lunaires ainsi que les satellites de jupiter, le confortant ainsi dans son idée que les concepts aristotéliciens sont définitivement morts. Il est à l'origine de la première loi sur la chute des corps et du principe de relativité du mouvement. Il sera le plus fervant défenseur de l'héliocentrisme ce qui lui vaudra en 1633 une convocation devant le tribunal de l'Inquisition, convocation aucours de laquelle il sera sommé d'abjurer les théories de Copernic. Galilée a vécu à une époque charnière qui a vu le déclin de la philosophie scolastique devenue spéculative et le renouveau de l'approche scientifique basée sur l'observation. A ce titre, il a été considéré comme un représentant éminent de ce renouveau. Ses démêlés avec l'institution ecclésiastique et sa condamnation en ont fait un emblème de l'indépendance de l'esprit scientifique vis-à-vis de tout dogmatisme religieux. Philosophie scolastique (ou philosophie chrétienne du Moyen Age). Elle consiste principalement à accorder les doctrines aristotéliciennes avec la religion. Elle est essentiellement dûe à saint Thomas d'Aquin (1225-1274). Pour le philosophe il ne doit y avoir aucune contradiction entre les vérités absolues de la foi et les vérités de la raison. Lorsqu'un conflit apparaît entre un dogme religieux et une affirmation de la raison, c'est que la soit-disant vérité rationnelle est dans l'erreur. |
|
Non, tout ne tourne pas autour de la Terre !
II) Référentiels Galiléens et Principe d'inertie
Si le mouvement et le repos sont des notions relatives, qu'adviendra-t-il d'un corps isolé dans l'espace, c'est à dire d'un corps soumis à aucune force ?
Contrairement à Aristote pour qui la force est responsable du mouvement, Galilée comprend qu'en l'abscence de forces, un corps peut bien sûr être immobile, mais peut également être animé d'un mouvement rectilligne uniforme (donc d'une vitesse) et ce, en vertu du caractère relatif du repos et du mouvement. Galillée (même si c'est Descartes qui l'a formulé correctement le premier) aboutit ainsi au principe d'inertie:
Par rapport à certains référentiels qualifiés de "réferentiels d'inertie" ou "référentiels galiléens", tout corps isolé est nécessairement immobile ou animé d'un mouvement rectiligne uniforme.
Ainsi pour Galilée, absence de forces n'implique pas automatiquement absence de vitesse; En fait, l'effet d'une force n'est plus une vitesse mais une accélération selon la première loi de Newton (Principia, 1687).
Le principe d'inertie, comme tout principe, ne se démontre pas mais appelle quelques commentaires. L'énoncé du principe d'inertie constitue une définition des référentiels galiléens et le dit principe postule leur existence. (Rappelons au passage qu'un référentiel est un solide de référence par rapport auquel on se base pour étudier le mouvement d'un autre corps. Il est donc nécessaire d'affecter à tout référentiel un système de coordonnées afin de repérer les positions du corps d'étude dans l'espace, ainsi qu'une horloge sans laquelle on ne peut définir les vitesses.)
Il faut bien comprendre que c'est en cherchant à vérifier expérimentalement le principe d'inertie qu'il est possible de construire des référentiels galiléens. Imaginons par exemple un corps suffisamment éloigné du système solaire et de toutes autres étoiles pour négliger l'attraction garvitationnelle exercée par ces masses. En première approximation, on peut considérer que notre corps est comme isolé, c'est à dire soumis à aucune force . Quel est son mouvement par rapport à l'ensemble des étoiles fixes constituant la voûte céleste ? Si on fait l'expérience, on peut vérifier que le corps restera effectivement immobile par rapport à la voûte céleste ou bien alors gardera un mouvement rectiligne et uniforme si ce corps était déjà en mouvement. Ainsi, et avec une très bonne approximation, l'ensemble des étoiles fixes apparaît comme un très bon candidat quant à la définition d'un référentiel galiléen. Il faut pourtant bien comprendre qu'il s'agit la d'une approximation, la meilleure que l'on connaisse, car en toute rigueur même les étoiles les plus lointaines de la voûte céleste ne sont pas parfaitement fixes mais changent légèrement de positions au cours des siècles, si bien que l'immobilité (ou le mouvement rectiligne uniforme) de notre corps par rapport au ciel étoilé ne peut être que partielle puisque temporaire.
La relativité des mouvements permet ensuite de construire tout un ensemble de référentiels galiléens; ils seront tous les référentiels immobiles ou animés d'un mouvement rectiligne uniforme par rapport à ces étoiles "fixes". Par exemple, le référentiel de Copernic défini par le soleil privé de son mouvement de rotation sur lui même, peut lui aussi être considéré comme galiléen sur une durée relativement importante dans la mesure où sur cette durée il reste quasiment immobile par rapport à la voûte céleste. De même, le référentiel géocentrique peut lui aussi être considéré comme galiléen sur une durée de quelques jours étant donné que pendant ce laps de temps son mouvement est quasiment rectiligne uniforme par rapport au référentiel héliocentrique lui même déjà considéré comme galiléen. Par approximations successives on voit que l'on peut ainsi construire toute une série de réferentiels galiléens. Néanmoins, on sent bien que la définition de ces référentiels galiléens reste malgré tout bien fragile ; D'une part il ne peut exister de corps parfaitement isolés dans un univers pourvu de matière, et d'autre part la voûte céleste qui constitue pourtant le meilleur référentiel galiléen que la nature semble offrir, n'en reste pas moins pour autant qu'un semblant de référentiel galiléen. Dès lors, le principe d'inertie tel qu'il est énoncé ne semble pas vraiment être un principe fondamental de la physique. On verra d'ailleurs par la suite que ces référentiels d'inertie sont définis différemment dans la théorie de la relativité générale d'Einstein ; ils sont tous les référentiels en chute libre dans le champ de gravité créé par l'ensemble des masses constituant l'univers et ce sera seulement par rapport à cette catégorie de référentiels que les mouvements des corps pourront être définis. (ce qui, comme on le verra plus loin, rejoint indirectement certaines conceptions "Machiennes" quant à la relativité des mouvements, conceptions ayant d'ailleurs fortement influencées Einstein dans l'élaboration de sa théorie de la relativité générale)
III) Le principe de relativité Galiléen
Puisque les notions de repos et de mouvements sont relatives, puisqu'aucune expérience ne permet de faire de différences, les lois de la physique doivent prendre la même forme dans tous les référentiels galiléens; C'est le principe de relativité. Il s'agit dès lors de trouver les changements possibles de systèmes de coordonnées laissant invariant les lois de la physique lorsqu'on passe d'un référentiel d'inertie à un autre.
En d'autres termes, le principe de relativité signifie que les équations décrivant n'importe quel phénomène physique doivent prendre la même forme dans tous les référentiels d'inertie. C'est ce qu'on appelle le principe de covariance qui est la traduction mathématique du principe de relativité.
Il s'agit dans un premier temps de se demander quelles transformations des systèmes de coordonnées laissent invariantes les lois physiques lors d'un changement de référentiel quelconque, ces référentiels étant immobiles les uns par rapport aux autres (mais affectés de systèmes de coordonnées différents). L'espace étant homogène et isotrope, toute translation et rotation du système d'axes doit laisser inchangée l'expression des lois physiques. De même, toute translation dans le temps doit laisser la loi invariante en raison de l'uniformité du temps. Enfin, le passage d'un référentiel galiléen à un autre doit également laisser les lois physiques invariantes. Les transformations mathématiques permettant de telles invariances portent le nom de "transformations de Galilée". Elles s'établissent à partir de 2 grandeurs supposées invariantes : l'élément de longueur "dl " et l'intervalle de temps "dt". La conservation de la longueur "dl" traduit simplement le fait que la taille d'un corps solide ne change pas lorsqu'on "passe" d'un référentiel inertiel à un autre. Quant à la conservation de l'intervalle de temps "dt", il traduit le fait que le temps doit s'écouler de la même manière dans tous les référentiels. De ces deux invariants, on obtient les équations de transformations des systèmes de coordonnées et à partir desquelles on déduit la loi d'additivité des vitesses, loi très bien vérifiée dans la vie quotidienne.
En conclusion, les lois physiques se doivent d'être invariantes vis à vis des translations et des rotations des systèmes d'axes, des translations dans le temps et des changements de référentiels galiléens.
Toutes les lois de la mécanique classique répondent bien évidement à ce critère dès lors qu'on considère également la force comme une grandeur invariante lors d'un changement de référentiel .
IV) Les lois de conservation en physique
|
Les symétries jouent souvent un rôle fondamental en physique puisqu'elles sont souvent à l'origine de certaines lois de conservations (voir le théorème de Noether). Telles sont le cas des lois de conservation de l'énergie (dont le physicien Helmoltz en est le précurseur), de la quantité de mouvement (Descartes) et du moment cinétique. En réalité, ces lois de conservation traduisent respectivement l'uniformité du temps, l'homogénéité et l'isotropie de l'espace. Elles peuvent se déduire du principe de moindre action dû à Hamilton et issu des travaux de Fermat , Maupertuis et Lagrange.
|
|
L'action
notée S, est l'intégrale en fonction du temps d'une fonction L(x,y,z,vx,vy,vz,t)
appelée "Lagrangien" du système. On peut montrer en
mécanique analytique que le mouvement réel d'un corps suivra les
trajectoires pour lesquelles l'action est minimale. Les équations différentielles
qui en résultent sont les équations de Lagrange : 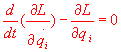
La première loi et la seconde loi de Newton peuvent en être déduites sous l'hypothèse qu'il existe des référentiels où l'espace est homogène et isotrope.
En second lieu, et du fait de l'uniformité du temps, la fonction de Lagrange ne dépendra pas de la variable temporelle si bien que les équations de Lagrange font apparaître une grandeur indépendante du temps et que l'on appelle "Energie". De même, le Lagrangien doit rester invariant sous les translations infinitésimales en raison de l'homogénéité de l'espace et là encore les équations font apparaître une nouvelle grandeur de nature vectorielle et qui reste inchangée au cours du mouvement : il s'agit du vecteur "quantité de mouvement" aussi appelé abusivement "impulsion". Enfin, l'isotropie de l'espace se traduira dans les équations de Lagrange par la conservation d'une autre grandeur: le moment cinétique.
La puissance de cette méthode va même au delà puisqu'elle permet de jeter un pont entre l'optique et la mécanique du point. Elle établit ainsi un lien entre les ondes et les corpuscules et c'est en se référant à la théorie de Hamilton-Jacobie puis en y introduisant le quantum d'action "h" que Schrodinger obtint sa célèbre équation:
Quelle interprétation faut-il donner à la fonction d'onde ? S'agit-il d'une onde de probabilité comme l'a suggéré Max Born en 1926 ou bien est-ce quelque chose de plus réaliste comme l'avait espéré Louis De Brooglie en 1927 puis Bohm après lui en 1952 (théorie de l'onde pilote: La fonction d'onde et les particules sont bien réelles, les ondes guidant les particules selon une loi dite "loi de l'onde pilote") ?
Peu soutenue par Einstein, pourtant fervent défenseur du réalisme en physique, la théorie de l'onde pilote fut rapidement oubliée et la seule interprétation encore donnée aujourd'hui est celle du cercle de Copenhague, position on ne peut plus antiréaliste...
V) Forces d'inertie, Référentiels "non Galiléens" et espace absolu
1°) "Dame Nature" ferait-elle des différences ?
Les référentiels non galiléens sont tous les référentiels non animés d'un mouvement rectiligne uniforme, c'est à dire tous les référentiels accélérés. Ces référentiels se doivent d'être traités différemment car les lois de la mécanique n'y sont plus valables ou du moins y prennent une forme légèrement différente. Afin de correctement décrire les phénomènes physiques ayant lieu par rapport à ces référentiels, il est nécessaire de rajouter à la seconde loi de Newton ce qu'on appelle des "forces d'inertie" et dont l'expression mathématique peut être déduite de la loi de composition des accélérations établie par le physicien Coriolis. Par exemple pour un référentiel en rotation, aux forces extérieures naturellement appliquées au corps d'étude, il faut dès lors tenir compte de la "force centrifuge" si l'on souhaite décrire correctement le mouvement de ce corps par rapport à un tel référentiel.
Les forces d'inertie:
|
|
|
Le véritable problème est de comprendre d'une part pourquoi la nature semble faire une distinction entre les référentiels accélérés et les réferentiels galiléens, obligeant ainsi les physiciens à utiliser deux catégories de lois différentes, et d'autre part de comprendre l'origine physique de ces forces d'inertie qui apparaissent si soudainement dès lors que le mouvement n'est plus rectiligne uniforme. A ces questions essentielles, le célèbre physicien Isaac Newton a su imposer pendant très longtemps son point de vue.
|
Isaac Newton (1642-1727), physicien et mathématicien anglais. En mathématique, il est surtout connu pour être le fondateur du calcul infinitésimal. En physique on lui doit l'unification de la mécanique céleste et terrestre via l'introduction d'une nouvelle interaction, l'interaction gravitationnelle qui agit à distance et de façon instantanée. On lui doit également la relation mathématique définissant la force comme responsable des modifications du mouvement ainsi que la loi des actions réciproques. En optique il réalise des expériences sur la dispersion de la lumière blanche à la traversée d'un prisme (1666) et introduit la notion de grains de lumières pour expliquer ce nouveau phénomène. Il est incontestablement un des plus grand esprit scientifique de toute l'histoire des sciences. Il fut inhumé à l'abbaye de Westminster aux côtés des rois d'Angleterre. On fit graver sur son mausolée une épitaphe en latin que l'on peut traduire comme suit : "Ici est enterré Isaac Newton, chevalier, qui par une force d'esprit presque divine, et des principes mathématiques à lui propre singuliers, a exploré le cours et les figures des planètes, les chemins des comètes, les marées de la mer, les dissimilitudes dans les rayons de la lumière, et, ce qu' aucun autre disciple n'a précédemment imaginé, les propriétés des couleurs ainsi produites. Diligent, sagace et fidèle, dans ses expositions de la nature, de l'antiquité et des Saintes Ecritures, il a défendu par sa philosophie la puissante et bonne majesté de Dieu, et a exprimé la simplicité de l'évangile à sa façon. Mortels, félicitez-vous qu'un si grand homme ait vécu pour l'honneur de la race humaine ! Il est né le 25 décembre 1642 et est mort le 20 mars 1727". |
S'il est clair depuis Galilée qu'il est impossible de caractériser de manière absolue les mouvements en translation rectiligne uniforme (les mouvements inertiels), il semble ne pas en aller de même en ce qui concerne les mouvements accélérés. En effet, quand on considère un corps tournant sur lui-même, il semble qu'on puisse caractériser l'existence d'un tel mouvement de façon intrinsèque, c'est à dire sans nullement faire appel à un autre corps de référence.
L'expérience des deux seaux présentée par Newton dans ses "Principia" en est une belle illustration :
De deux seaux 1 et 2, pleins d'eau, l'un (1) est en rotation et pas l'autre (2); la surface de l'eau du premier seau se déforme en s'élèvant sur ses bords et non celle de l'autre.
Lorsqu'au départ le premier seau se met à tourner, la surface de l'eau reste plane, puis, peu à peu en raison de sa viscosité, l'eau se met finalement à tourner à la même vitesse que le seau (dès lors, sa surface n'est plus plane mais correspond à celle d'une paraboloide) si bien qu'ils deviennent immobiles l'un par rapport à l'autre comme dans le cas du seau n°2. Pourtant, la surface de l'eau est plane dans un cas et non dans l'autre..
Newton pose alors la question suivante : qu’est-ce qui fait monter l’eau sur les parois du seau ? Son mouvement, sans doute. Mais mouvement par rapport à quoi ? Pas par rapport au seau évidemment, puisque lorsqu’ils sont immobiles l’un par rapport à l’autre, la surface de l'eau est toujours incurvée. Newton répond à sa propre question : l’eau est en mouvement par rapport à l’espace absolu et c’est ce qui explique la courbure de sa surface.
Pour Newton, l'élévation de la surface de l'eau s'explique par l'apparition d'une force centrifuge qui émane d' un espace absolu toujours similaire et immobile et sans relations aux choses externes (c'est à dire un espace dépourvu de toute matérialité). Selon Newton, cet espace absolu serait un peu comme une scène de théatre à l'intérieur de laquelle les corps sont, se meuvent ou restent immobiles.
Ainsi, et contrairement aux mouvements inertiels pour lesquels la prise de conscience du mouvement ne peut se faire sans référence à un autre corps, les mouvements accélérés semblent définissables par une expérience purement locale.
Pour Newton, c'est l'existence même de cet espace absolu qui est à l'origine des forces d'inertie qui apparaissent sur les corps accélérés, ce qui permet dès lors de caractériser de façon absolue ces mouvements non inertiels. Ainsi, en théorie Newtonienne, l'existence des forces d'inertie est une preuve de l'existence et du caractère absolu de l'espace puisque c'est celui-ci qui est responsable de l'apparition des forces d'inertie (on semble un peu tourner en rond...)
Pour faire simple, l'espace absolu de Newton est un cadre de référence éternel et immuable, responsable des forces d'inertie et par rapport auquel on pourrait donc mettre en évidence les mouvements accélérés puisque ces "dits mouvements" sont justement assujetis à de telles forces.... C'est donc finalement par rapport à cet espace absolu qu'on pourrait affirmer qu'un corps tourne ou accélère. Quelques cent ans plus tard (1798) c'est toujours par rapport à ce même espace absolu que le plan du pendule de Foucault était supposé rester fixe; Expérience démontrant ainsi pour la première fois que la Terre tourne bien sur elle même.
 plus
d'infos sur Léon Foucault : http://expositions.obspm.fr/L.Foucault/intro.html
plus
d'infos sur Léon Foucault : http://expositions.obspm.fr/L.Foucault/intro.html
Pour conclure, la relativité des mouvements n'est, selon Newton, que partielle puisque restreinte aux mouvements rectilignes et uniformes.
2°) L'espace absolu : une réalité ?
Positivisme : philosophie selon laquelle la science se doit seulement d'expliquer (par le biais des sens et de l'expérience) le "comment" des choses et non le "pourquoi" qui est ainsi laissé au domaine non scientifique de la théologie ou de la métaphysique. Le positivisme doit seulement reposer :
Malgré la logique apparemment implacable des réponses apportées par Newton, les critiques ne se feront pourtant pas attendre ! Pour Leibniz avec qui Newton avait déjà eu un différent quant à la paternité du calcul infinitésimal, définir un espace indépendamment des objets qu'il contient ne peut avoir de sens. Malgrè tout, Newton réussira à imposer ses idées pendant plus de deux siècles et il faudra attendre les nouvelles idées d'origine positivistes du philosophe et physicien Ernst Mach pour que les choses soient enfin envisagées différemment.
Pour Mach, le mouvement d'un corps ne peut être défini que relativement à un autre corps et non par rapport à un espace totalement abstrait puisque dépourvu de toute matérialité. D'ailleurs, comment parler d'espace sans aucune référence à des corps matériels ? Comment déterminer la position d'un corps dans un tel espace si on ne peut y inscrire une marque de référence ? Comment dès lors définir des notions telles que la vitesse et l'accélération ? Pour le philosophe, l'espace vide de Newton n'a absolument aucune réalité !
Si on ne peut définir un mouvement que par rapport à un autre corps, les notions de repos et de mouvement ne peuvent être que relatives puisque tout n'est finalement qu'une question de point de vue. Contrairement à Newton qui affirme que le mouvement accéléré peut être caractérisé de façon absolue, les nouvelles conceptions de Mach permettent dorénavant d'imaginer que n'importe quel corps est immobile mais que ce sont par contre les autres corps de référence qui bougent, tant est si bien qu'il devient impossible de trancher catégoriquement entre repos et mouvement.
Selon Mach, la nature ne doit pas permettre de faire de distinctions entre le repos et le mouvement, qu'il soit rectiligne uniforme ou même accéléré. Tout mouvement ne peut être que relatif !
Pourtant, et c'est une réalité, des forces d'inertie apparaissent lorsqu'un corps tourne ou accélère alors qu'on devrait toujours pouvoir l'imaginer immobile en raison de la relativité générale de tous les mouvements. Comment rétablir alors la supposée symétrie entre repos et mouvement accéléré ? Selon Mach, il doit nécessairement apparaitre des forces d'inertie lorsque le corps est supposé immobile mais que l'on imagine en retour que ce sont les autres corps de référence qui accélèrent. Toujours selon Mach, la Terre par exemple, devrait toujours être "enflée" au niveau de l'équateur si on la suppose immobile mais que l'on imagine en retour la voûte céleste tournant autour d'elle (il s'agit d'une situation certes peu tangible mais néanmoins tout à fait imaginable). Pour Newton au contraire, la Terre ne serait soumise à aucune force centrifuge et serait donc parfaitement sphérique si réellement la voûte céleste tournait autour d'elle, car même si l'illusion peut sembler parfaite, il n'en resterait pas moins vrai que la Terre serait toujours immobile par rapport à l'espace absolu si bien qu'aucune force d'inertie ne pourrait apparaître. La symétrie du problème est bonc brisée si on imagine l'espace absolu comme responsable des forces d'inertie.
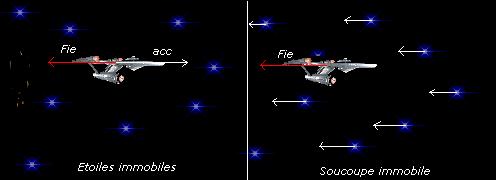

D'après Mach, l'origine des forces d'inertie ne peut pas être expliquée par l'action de cette espace phantôme introduit par Newton car de part son étrange facultée à générer les forces d'inertie, la symétrie entre repos et mouvement accéléré est irrémédiablement brisée. Comment d'ailleurs immaginer qu'un espace totalement vide puisse agir sur les corps matériels sous seul prétexte qu'ils accélèrent par rapport à lui ? Par quel enchantement cela serait-il possible?
Pour conserver la symétrie requise par une relativité totale du mouvement, il faut concevoir les forces d'inertie comme ne pouvant émaner que des corps de référence et par rapport auxquels on peut justement prétendre accélérer, ces corps étant l'ensemble des masses constituant l'univers. Or toujours selon Mach, la seule possibilité pour ces masses d'agir à distance sur les corps accélérés est la force de gravité. Ainsi, les forces d'inertie ne peuvent trouver leur origine que dans l'attraction gravitationnelle exercée par l'ensemble des masses de l'univers. En supposant les forces d'inertie de nature gravitationnelle, la symétrie requise entre repos et accélération est enfin conservée. Selon Mach, un corps tournant sur lui-même dans un espace vide de matière ne peut d'ailleurs subir aucune force centrifuge (puisque celle-ci est de nature gravitationnelle) tout comme s'il était parfaitement immobile si bien que son mouvement de rotation ne pourrait nullement être mis en évidence et serait donc totalement indistinguable du repos parfait. (En fait Mach va même jusqu'à affirmer qu' un corps ne peut ni tourner, ni accélérer dans un espace vide comme celui imaginé par Newton, la notion de mouvement ne pouvant être que relative)
Il est intéressant de noter que si l'on accepte intégralement les idées de Mach, tout corps animé d'un mouvement accéléré peut, de manière équivalente, être considéré comme au repos mais soumis aux forces de gravité émanant des autres corps de l'univers et accélérant relativement à lui. Inversement, tout corps apparemment immobile et sur lequel agiraient des forces gravitationnelles peut tout aussi bien (symétrie oblige) être imaginé comme accélérant de façon appropriée par rapport aux autres corps de l'univers.
Pour conclure, selon les principes de Mach, les mouvements accélérés tout comme les mouvements inertiels ne peuvent être que relatifs ; Tout n'est qu'une question de point de vue.
Malgré tout et même si Mach ramène l'accélération à un concept relatif, il n'en reste pas moins vrai que la nature semble toujours distinguer le mouvement rectiligne uniforme du mouvement accéléré. En effet, les nouvelles conceptions de Mach ne nous expliquent pas pourquoi des forces gravitationnelles apparaissent sur les corps accélérés et non sur les corps en mouvement rectiligne uniforme.
C'est pourtant en s'appuyant sur les idées novatrices de Mach qu'Albert Einstein construira entre 1905 et 1915 sa théorie de la relativité générale même si au final les résultats de la théorie ne seront que très partiellement en accord avec les conceptions du philosophe quant à la véritable origine des forces d'inertie.
NB: Les équations de la relativité générale devraient par exemple exclure toutes
solutions correspondant à un univers vide de matière et dans lequel
on pourrait modéliser un corps unique et tournant sur lui même, ce qui n'est pas le cas..De façon plus générale, le principe de Mach stipule qu'il ne devrait même pas exister de champ métrique (donc pas d'espace-temps) en l'abscence de matière ce que l'on peut traduire mathématiquement par : ![]() (condition de Pauli sur le principe de Mach)
(condition de Pauli sur le principe de Mach)
La métrique pseudo-euclidienne de Minkowski est pourtant solution de l'équation d'Einstein en l'abscence de matière...Il est toutefois possible d'incorporer le principe de Mach à la théorie d'Einstein via l'introduction de champs scalaires si on accepte de faire fi du principe d'équivalence "fort" (voir chapitre théories tenseur-scalaire en RG)
VI) La théorie de la relativité restreinte
1°) L 'éther, une hypothèse superflue
Si l'espace absolu de newton semblait pour beaucoup dénué de toute réalité, les physiciens du XVIII et XIX siècle (et même Huygens avant eux) lui donnèrent un peu plus de consistance en l'emplissant d'une substance invisible : l'éther. Cette substance, elle aussi plutôt phantomatique, était sensée assurer la propagation des ondes lumineuses dont la réalité ne faisait plus guère de doutes depuis les travaux de Young puis Fresnel. Elle devait à la fois être rigide pour expliquer la très grande vitesse de propagation des signaux lumineux tout en étant facilement pénétrable pour ne pas entraver les mouvements réguliers des différentes planètes.
Si les incertitudes sur l'existence réelle de cette éther semblaient quelque peu oubliées, la question fut remise à l'ordre du jour après une analyse détaillée des équations de Maxwell et de l'équation d'onde qui en résulte.
|
|
James Clerk Maxwell (1831-1879) : Physicien Ecossais. Une partie importante de ses travaux concerne la cinétique des gaz et la thermodynamique où il associe la chaleur au mouvement des molécules. Il est surtout connu pour son traité d'électricité et de magnétisme qui paraîtra en 1873 ; Il s'agit d'une formidable synthèse des travaux de Faraday et Ampère où tous les phénomènes électriques et magnétiques sont résumés en 4 équations et dont le développement conduit à l'apparition d'ondes électromagnétiques. La confirmation expérimentale viendra quelques années plus tard en 1888 avec la découverte par H.Hertz de l'émission et de la détection de ces ondes électromagnétiques. |
Ces équations font apparaître la vitesse de propagation "c" des ondes électromagnétiques comme étant une constante puisque reliée à deux autres constantes de la physique et caractéristiques du vide : la "permittivité magnétique mo" et la "permittivité électrique eo ". De part la nature même de cette relation, "c" semble être définie indépendamment de la vitesse des sources lumineuses contrairement à ce qui est prévu selon les lois de la cinématique classique. Dès lors une question se pose : Dans quel référentiel cette vitesse est-elle définie ? Est-ce seulement la vitesse de la lumière dans un référentiel particulier, réduisant ainsi la validité des équations de Maxwell à ce seul référentiel?
Pour la plupart des physiciens de l'époque, cette vitesse est celle de la lumière dans le vide c'est à dire par rapport l'éther (i.e l'espace absolu de Newton). Ainsi, les équations de Maxwell semblent n'être valables que dans ce référentiel privilégié ce qui est d'ailleurs en accord avec le fait qu'elles ne sont pas invariantes sous une transformation de Galilée (démonstration). Contrairement aux lois de la mécanique, les équations régissant les phénomènes électromagnétiques ne satisfont donc pas au principe de relativité pourtant si cher à Mach et bien d'autres.
La conclusion est donc simple et présente de plus l'avantage de pouvoir mesurer le mouvement des autres référentiels par rapport à l'éther, ce qui lui donnerait enfin une certaine réalité pour ne pas dire une réalité certaine. La démarche est simple ; Il suffit de mesurer la vitesse de la lumière depuis la Terre (référentiel à priori en mouvement par rapport à l'éther) dans deux directions opposées (ou perpendiculaire) pour en déduire, via la loi d'addivité des vitesses, la vitesse V de la Terre par rapport à l'éther. Dans la première direction (celle du mouvement de la Terre) on doit trouver pour la vitesse de la lumière la valeur c'= c + v et dans l'autre direction on doit mesurer c''= c-v.
|
(1852-1931)
|
Les expériences se suivent et se ressemblent malgré une précision toujours accrue ( cf l'expérience d'interférométrie de Michelson et Morley en 1887). Les résulats sont sans appel..quelque soit la direction dans laquelle on souhaite mesurer la vitesse des ondes lumineuses, quelque soit le référentiel depuis lequel on la mesure, quelque soit la vitesse de la source émettrice, on trouve toujours c=299 792 458 m/s ! Ainsi et contrairement à toute attente, il semble impossible de mettre en évidence cet éther. Cet éther indissociablement lié à l'espace absolu introduit par Newton semble finalement dépourvu de toute réalité puisque physiquement impossible à mettre en évidence. Dans le but de sauver malgré tout cet éther si fondamental à la cohérence des théories mécaniques et éléctromagnétiques, Fitzgerald et Lorentz proposèrent d'admettre l'existence d'une contraction des corps matériels provoquée par leur mouvement dans l'éther afin de concilier le résultat négatif de l'expérience de Michelson : cette contraction, supposée réelle pour les deux physiciens, aurait diminué la longueur des corps dans le sens de leur mouvement afin de compenser exactement les effets du mouvement sur la propagation de la lumière. Cette ingénieuse hypothèse avait évidemment un caractère artificiel et semblait uniquement imaginée pour masquer un échec. Ce fut on le sait Einstein, qui par un admirable effort de pensée, put trouver la solution du problème (1905)
|
|
Albert Einstein (1879-1955): Il publie dans les Annales de Physique quatre articles exceptionnels. Dans le premier, il introduit la notion de photon, particule associée au champ élecromagnétique, d'énergie E = hv. Il tire cette conclusion d'une analyse de l'effet photoélectrique. Dans le second article, il traite le mouvement Brownien dans un formalisme probabiliste apportant ainsi une nouvelle preuve quant à la réalité des atomes. Dans le troisième, il pose les fondements de la relativité restreinte remettant en cause l'indépendance de l'espace et du temps. Enfin dans le dernier article, il établit la célèbre équation E= m.c2 qui traduit l'équivalence enre la masse et l'énergie. Il publiera également en 1916 une théorie encore plus révolutionaire, la "relativité générale" où le champ de gravitation y est interprété comme une courbure de l'espace-temps. Il recevra en 1921 le prix nobel de physique pour sa théorie de l'effet photoélectrique. Toute sa vie durant il refusera l'interprétation probabiliste de la mécanique quantique défendue par le cercle de Copenhague autour de Niels Bohr. |
|
2°) Distances et durées: 2 grandeurs finalement relatives
Dès l'âge de 16 ans Einstein s'interrogeait sur ce que verrait un observateur porté par une onde lumineuse. Selon lui, tout observateur poursuivant un rayon lumineux à la vitesse "c" doit percevoir la lumière comme un champ électromagnétique figé dans le temps (car s'il observe l'onde osciller c'est qu'elle se propage encore d'après l'équation d'onde. Or si elle avance encore c'est qu'elle va plus vite que sa supposée vitesse de propagation ce qui est bien sûr paradoxal). Pour Einstein, cette simple expérience de pensée l'ammène à conclure qu'il est physiquement impossible d'atteindre et même dépasser la vitesse de la lumière (ce qui est pourtant autorisé théoriquement si l'on se réfère aux transformations de Galilée et à sa loi de composition des vitesses). Il fera quelques années plus tard de cette impossibilité à dépasser cette vitesse un postulat. Pour Einstein, la vitesse de lumière est une vitesse limite. De cette expérience, on peut déjà entrevoir le caractère relatif du temps : tout observateur se déplaçant à la vitesse de la lumière ne doit plus "voir" le temps s'écouler, il est comme "gelé".
De l'invariance de la vitesse de la lumière, Einstein saura tirer toutes les conclusions logiquement possibles. Il pratiquera ainsi un grand nombre d'expériences de pensée qui l'ammèneront finalement à rejeter catégoriquement le caractère absolu des notions de temps et de longueurs. En fait c'est une analyse de la notion de simultanéitée qui conduit Einstein à rejeter le caractère absolu du temps. Il démontre que la simultanéité de deux événements est relative au référentiel d'étude.
a) La non simultanéité de 2 évènements
|
Imaginons un wagon de longueur "2L" se déplaçant de la gauche vers la droite, à vitesse constante v, et au milieu duquel se trouve une lampe éteinte. Lorsque la lampe passe juste devant les yeux d'un observateur immobile situé sur le quai de la gare, celle-ci s'allume et des photons partent dans toutes les directions avec la vitesse constante c, que cette vitesse soit mesurée depuis l'intérieur du wagon ou depuis l'extérieur, conformément au résultat négatif de l'expérience de Michelson. Pour un passager situé au milieu du wagon, il ne fait guère de doute que les photons atteindront les deux extrémités du wagon au même instant puisque les distances à parcourir pour les photons seront rigoureusement les mêmes ( à savoir L) vu que la lampe est au milieu du wagon. Pour l'observateur sur le quai, les photons n'atteindront pas les deux extrémités du wagon au même instant. En effet, pour l'observateur immobile, les photons ont une distance plus grande à parcourir pour toucher l'extrémité droite du wagon du fait que celui-ci avance. Inversement les photons se déplaçant vers la gauche auront une distance plus petite à parcourir et atteindront le mur gauche du wagon avant ceux partis vers la droite. Ainsi, si la vitesse de la lumière est une constante, deux évènements simultanés pour une personne en mouvement ne le sont plus pour une autre immobile. La notion de simultanéité dépend du référentiel dans lesquel on se place ce qui n'était pas le cas dans la conception galiléenne. (voir démonstration)
Ci-contre: l'expérience du train telle que présentée par A.Einstein:
|
En mécanique classique, la notion de simultanéité était une conséquence du concept de temps absolu, c'est à dire d'un temps s'écoulant de façon identique dans tous les référentiels. En relativité restreinte, cette notion, comme d'ailleurs celle de "chronologie" de 2 évènements devient relative:
Imaginons qu'une supernovae explose dans la galaxie d'Andromède et qu'une météorite s'écrase sur Terre, ces 2 évènements étant non liés causalement.
Les 2 phénomènes sont-ils simultanés? L'un s'est-il déroulé avant l'autre? L'observateur terrestre verra la météorite tomber avant l'explosion alors que l'observateur situé dans la galaxie d'Andromède verra la supernovae exploser avant la chute.
On peut également trouver un 3ième observateur pour qui les 2 phénomènes auront lieu simultanément. Du fait de la vitesse finie de l'information, chaque observateur voit les évènements survenir à différents moments en fonction de sa position et de sa vitesse par rapport aux autres. Le "présent" d'un observateur peut correspondre au "futur" d'un autre et réciproquement. Dès lors, on voit difficilement comment la notion de temps universel pourrait exister.
Avec Einstein, la longueur d'une règle rigide devient elle aussi un concept relatif : il y a contraction des longueurs d'un repère inertiel à un autre.
Pour Lorentz, cette contraction des longueurs est un phénomène réel alors qu'il ne s'agit en fait que d'un effet de perspective (idem pour la dilatation des durées).
Contractions des longueurs et dilatations des durées ne sont en fait qu'apparentes comme on le verra plus loin.
b) Les transformations de Lorentz-Poincaré
Dans sa jeunesse, les lectures de Mach ont profondement influencé Einstein. Tout comme Mach, Einstein est convaincu que la notion de mouvement ne peut être que relative, niant de fait l'existence d'un repère absolu comme l'espace de Newton. Les expériences négatives de Michelson et Morley vont dans ce sens puisqu'elles sont incapables de rendre compte d'un quelconque mouvement des autres référentiels par rapport à celui de l'éther. Pour Einstein, éther et espace absolu sont des concepts vides de sens, ils ne sont tout simplement que chimères !
En définitive, les équations de Maxwell ne sont pas seulement valables dans cet hypothétique référentiel privilégié comme on aurait pu le penser, elles sont aussi valables dans tous les référentiels inertiels. En vertu du principe de relativité, maintenant étendu aux phénomènes électromagnétiques, si l'équation d'onde de Maxwell n'est pas invariante sous une transformation de Galilée c'est que cette loi de transformation des systèmes de coordonnées est nécessairement erronée. Ainsi, après avoir compris que les notions de temps et d'espace étaient finalement relatives, Einstein aboutira en 1905 aux transformations de Lorentz, (transformations d'ailleurs déjà établies par Poincaré la même année) qui laissent invariantes les équations de Maxwell et l'équation d'onde qui en résulte.
Remarque:
En réalité, c'est une expérience d'électromagnétisme (mouvement relatif d'un aimant par rapport à une bobine) qui pousse Einstein à remplacer les transformations de Galilée par de nouvelles transformations du système de coordonnées. En effet, suivant que l'aimant se déplace par rapport à la bobine ou alors l'inverse, le phénomène observé (à savoir l'apparition d'un courant induit dans la bobine) est parfaitement identique bien qu'il soit mathématiquement décrit de façon différente ; Dans le premier cas lorsque l'aimant bouge, le flux magnétique à travers la bobine change et un champ électrique apparait dans celle-ci donnant ainsi naissance à un courant électrique :
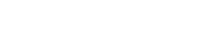
Dans le second cas, lorsque la bobine se déplace vers l'aimant, c'est la force de Lorentz qui est responsable de l'apparition d'un courant électrique.
![]()
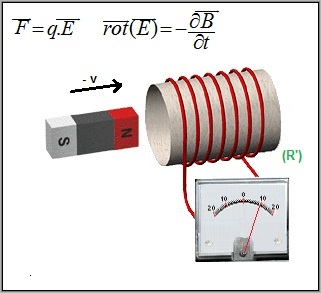 expérience identique à:
expérience identique à: 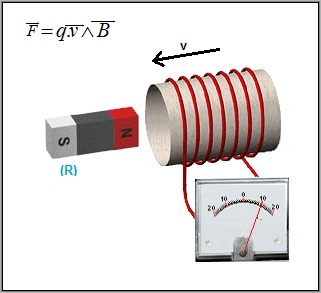
Il semblerait donc que cette expérience d'électromagnétisme permette de savoir si c'est l'aimant qui bouge ou bien la bobine puisqu'il apparait un champ électrique dans la première situation et non dans la seconde. Pourtant, en vertu du principe de relativité du mouvement énoncé par Galilée, ces deux expériences devraient être tout à fait symétriques c'est à dire physiquement non distinguables. Selon Einstein, les équations mathématiques traduisant ces deux expériences pourtant physiquement équivalentes, devraient donc être identiques ou tout du moins devraient être" transmutables" l'une en l'autre via la loi de transformation des champs E et B qui découlent de la loi d'additivité des vitesses de Galilée, et ceci, sans engendrer de contradictions. Ce n'est pourtant pas le cas:

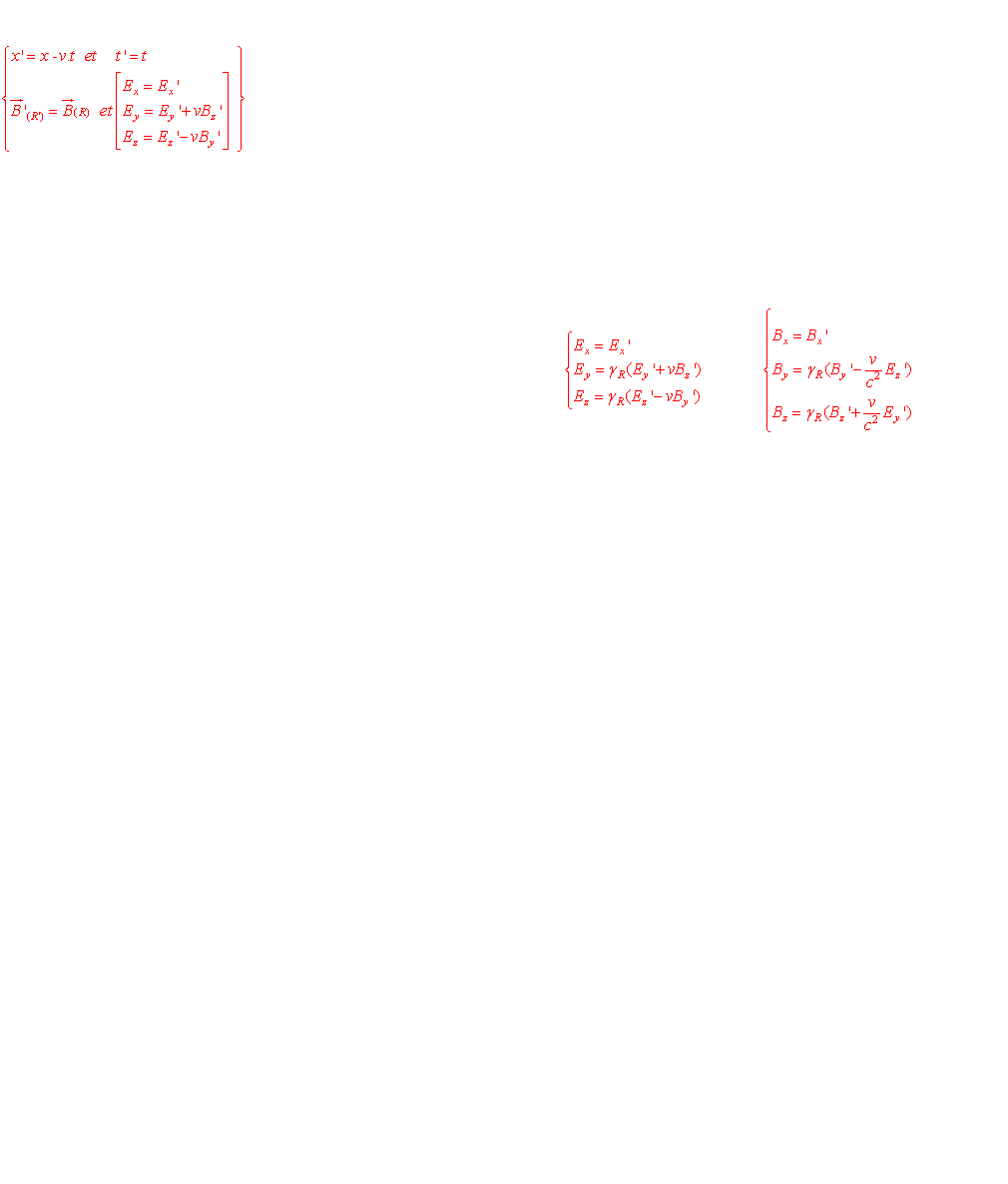
Persuadé que ces deux expériences sont véritablement indistinguables car symétriques, Einstein rejette la véracité des transformations de Galilée et les modifie pour aboutir aux transformations de Lorentz. Historiquement parlant, ce n'est donc pas vraiment l'expérience de Michelson et l'invariance de la vitesse de la lumière qui pousse Einstein vers sa future théorie de la relativité restreinte mais bien plutôt sa foi inébranlable envers le principe de relativité des mouvements. Pour Einstein, l'expérience de Michelson est davantage une vérification expérimentale de sa théorie plutôt qu'un point de départ dans la construction de ses idées nouvelles.
On peut également obtenir la loi de transformation directement depuis l'équation d'onde de Maxwell en cherchant une transformation linéaire du système de coordonnées laissant invariants les opérateurs de l'équation d'onde.

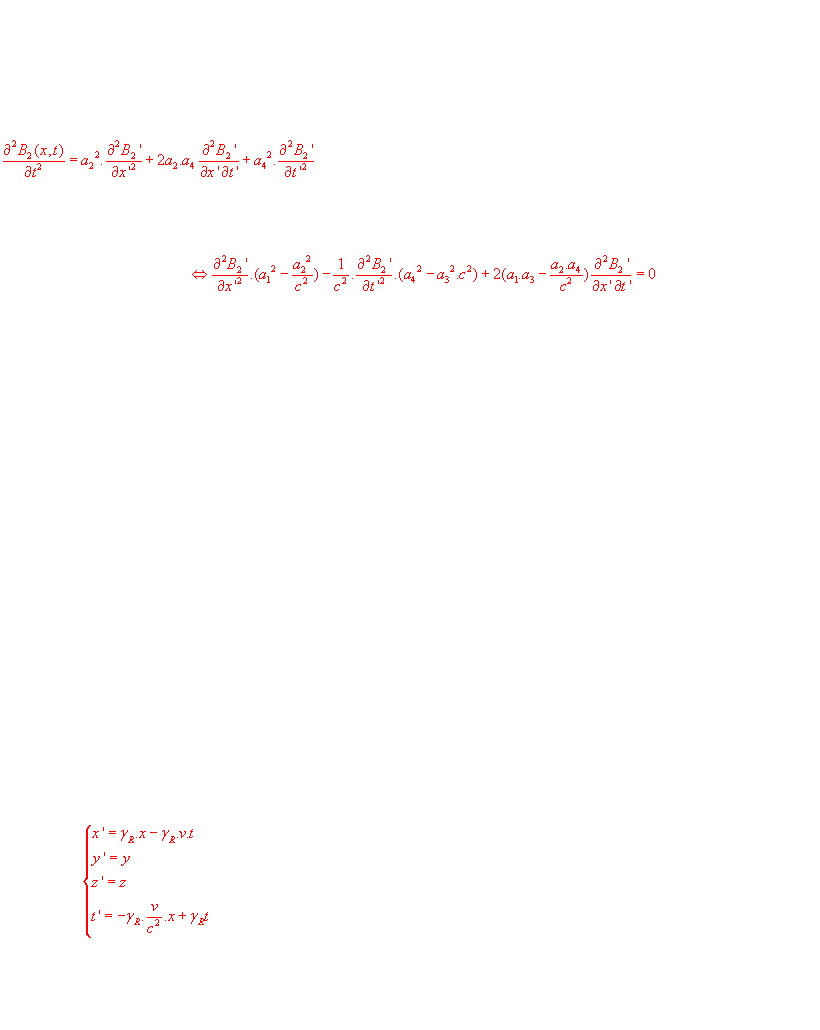
Remarque: Comme l'a montré Levy-Leblond, le second postulat (invariance de c) n'est pas nécessaire pour obtenir la loi de transformation de Lorentz. Le principe de relativité, accompagné de l'hypothèse que l'espace est homogène et isotrope, suffit à lui seul. Le principe de relativité se traduit mathématiquement par le fait que les lois de la nature doivent garder la même forme quelque soit le système de coordonnées choisi lorsqu'on passe d'un référentiel inertiel à un autre. Avec ces seules conditions, les lois de transformations les plus générales des systèmes de coordonnées doivent posséder une structure de groupe (comme l'avait déjà montré Poincaré) et dont les transformations de Lorentz ne sont qu'un cas particulier correspondant au cas où la vitesse limite est celle de la lumière.
En fait, la constante" c" qui joue le rôle de vitesse limite dans les lois de transformations générales n'apparait pas nécessairement comme devant être la vitesse de la lumière. Cette constante est égale à la vitesse de la lumière seulement si le photon possède une masse nulle (ce qui est à priori le cas). Voir la démonstration
c) Contraction des longueurs et "dilatation" des durées
Les phénomènes de contraction des longueurs et de dilatation des durées précédemment mentionnnés, se déduisent bien évidemment des transformations de Lorentz comme le montrent les deux exemples ci dessous:
Supposons une règle de longueur L'o =
Dx ' immobile
dans (R') en
mouvement rectiligne uniforme par rapport à (R) .
Pour connaître la longueur L = Dx
de cette règle dans le référentiel
(R) ={Oxi}, il faut déterminer la différence d'abscisses
de ses deux extrémités au même instant dans (R). La relation ![]() permet d'exprimer
facilement cette condition (Dt =0)
permet d'exprimer
facilement cette condition (Dt =0)

![]()
Ainsi dans le référentiel (R) la règle semblera plus petite qu'elle ne l'est dans R'.

Elle est souvent illustrée par l'expérience suivante où deux observateurs évaluent le laps de temps écoulé pour qu'une particule de lumière fasse un aller-retour entre deux miroirs face à face (l'un est disposé sur le plancher d'un wagon en mouvement et l'autre est attaché au plafond de ce même wagon).
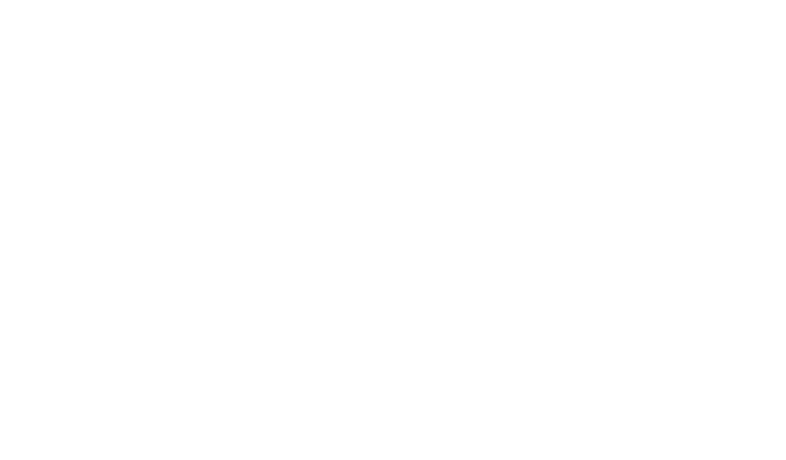
L'observateur immobile sur le quai de la gare mesure un laps de temps plus grand que celui situé dans le train en mouvement. Autrement dit, il trouve que le même phénomène physique dure plus longtemps.
Comme mentionné tout à l'heure, ce phénomène de dilatation des durées se déduit directement des transformations de Lorentz:
Soit Dt' le laps
de temps écoulé entre deux signaux émis par une horloge
immobile par rapport à (R') ( Dx '=
0 ). Soit Dt le laps
de temps écoulé entre la réception de ces deux signaux
dans (R) . La relation (2) en permutant t en t', x en x' et v en -v devient :
![]() et pour Dx' = 0 elle
donne :
et pour Dx' = 0 elle
donne :

![]()
Ainsi, mesuré depuis (R), le laps de temps Dt entre deux signaux de l'horloge paraît plus long que dans (R'). On dit qu'il y a dilatation des durées. On observera exactement le même phénomène si on se place dans (R'), c'est à dire qu'on observera également une dilatation des durées par rapport à (R).
Il s'agit d'un effet expérimentalement vérifiable comme le prouve la désintégration des muons. Ces électrons lourds découverts par Powell en 1937 se désintègrent en 2,2.10 - 6s lorsqu'ils sont au repos. Avec une durée de vie aussi courte il ne peuvent franchir que 600 m en se déplaçant à la vitesse de la lumière or l'expérience prouve qu'ils arrivent sur Terre alors qu'ils se forment dans les hautes couches de l'atmosphère situées à plusieurs dizaines de km du sol terrestre . Mesurée depuis notre référentiel terrestre, leur durée de vie vaut Dt = g.Dto >> Dto (car leur vitesse avoisine 99% de la vitesse de la lumière lorsqu'ils se forment) ce qui leur laisse le "temps" de parcourir bien plus de 600 m.
En mécanique classique, il était possible d'assigner une durée bien défini à tout phénomène physique. En relativité restreinte, cela n'est plus possible: chaque observateur en mouvement relatif par rapport à l'autre affecte à un phénomène physique une durée différente, chacune étant tout aussi valable que l'autre.
Notons également comment les transformations de Lorentz lient de façon nouvelle, l'espace et le temps comme le montre l'équation (1).
Supposons par exemple que deux évenements aient lieu au même instant dans (R') (Dt'=0) mais en des lieux différents Dx' ¹0 , alors d'après (1):
![]()
Ainsi, les deux évenements qui étaient simultanés dans (R') ne le sont plus dans (R) mais dépendent de la distance Dx' séparant les deux évenements dans (R').
3°) Un seul et unique concept: l'espace-temps !
Non seulement, les notions d'espace et de temps sont relatives mais les voilà maintenant liées l'une à l'autre. Désormais il ne faut plus parler d'espace et de temps séparemment comme à l'époque de Newton mais seulement d'espace-temps, seul concept qui garde un caractère absolu (voir Minkoswki).
Ainsi, longueurs et durées ne sont plus des grandeurs intrinsèques mais dépendent du repère dans lequel on les mesure: elles sont relatives. Dans la mesure où ces grandeurs ne sont pas intrinsèques, il est bien difficile de les utiliser correctement comme "observables physiques". Et pourtant, ce qu'il faut à un physicien ce sont justement des grandeurs physiques qui soient définies indépendamment de tout repère et que l'on puisse ensuite projeter sur le repère précis dans lequel on travaille et où elles seront alors observées. Quelle est donc cette grandeur physique qui restera invariante dans tous les référentiels galiléens et qui seule gardera un véritable sens physique?
On l'a dit, il ne peut s'agir du temps-coordonnée tout seul, ni non plus de la distance-coordonnée puisque leurs valeurs dépendent du référentiel. Ces deux grandeurs sont donc dénuées de sens physique. Si les lois de transformations de Galilée se construisent depuis les deux invariants fondamentaux que sont la longueur d'un corps et la durée d'un phénomène (deux grandeurs observables en mécanique classique) , depuis quel(s) invariant(s) les transformations de Lorentz peuvent-elles se déduire ?
Dans un premier temps, on sait que la grandeur mathématique recherchée doit être invariante sous une transformation de Lorentz, transformation qui relie l'espace et le temps. La grandeur recherchée doit donc être un mélange du temps-coordonnée (t) et de la distance-coordonnée ( x2 + y 2 + z 2)
En second lieu, il doit s'agir d'une grandeur observable comme l'était la longueur d'un corps ou la durée en mécanique classique.
C'est à Minkowski que l'on doit l'introduction de cette grandeur qui porte le nom de "temps propre" et qui est noté "to". Il s'agit du temps mesuré dans le référentiel constamment lié au corps; C'est le temps indiqué par sa "montre-bracelet" où encore le temps rythmé par les battements de son coeur à supposer que ce corps soit vivant et que les battements soient réguliers. il s'agit donc d'une grandeur observable, intrinsèque, et qui ne doit évidemment pas changer lorsqu'on passe d'un référentiel à un autre, sinon ce corps ne vieillirait pas de la même manière suivant le référentiel dans lequel il se trouve ce qui est bien sûr absurde.
Comme l'avait déjà immaginé Einstein à l'âge de 16 ans, ce temps propre est figé pour les corps se déplaçant à la vitesse de la lumière, ce qui se traduit par : Dto = 0 . Or il existe une grandeur, mélange de temps-coordonnée et de distance-coordonnée, qui prend constamment la valeur 0 pour la lumière et qui reste bien invariante sous une transformation de Lorentz ; C'est la grandeur : c2t2 - (x2 + y2 + z2 ).
Minkowski la notera sous forme infinitésimale, il s'agit de la grandeur : (c.dto)2= ds2 = c2dt2 - (dx2 +d y2 + dz2 )
C'est une sorte de généralisation du théorème de Pythagore dans l'espace-temps à 4 dimensions et où "ds" représente la "distance quadridimensionnelle".
Notons pour finir qu'il s'agit d'une grandeur extrêmement importante puisque c'est la seule grandeur dont la valeur ne dépend pas du référentiel d'étude et donc du système de coordonnées que l'on choisit. Ce sera d'ailleurs l'un des futurs piliers de la théorie de la relativité générale.
Remarque: La loi de transformation de Lorentz peut aussi être obtenue en cherchant les formes linéaires laissant invariante la pseudo-distance ds2
|
|
Hermann Minkowski (1864-1909) : Professeur de mathématique à Bonn puis Zurich où il a pour élève A.Einstein qu'il qualifiera de "chien paresseux". Ces travaux concernent essentiellement les mathématiques pures. Il participe en 1905 à des séminaires sur l'électromagnétisme et sur la relativité. Il démontre alors que les idées d'Einstein et Lorentz seraient formellement mieux traitées en utilisant un espace à 4 dimensions où l'espace et le temps ne seraient plus séparés. Il démontre également en 1908 que l'électromagnétisme est correctement décrit dans cet espace à 4 dimensions. De la relativité d'Albert Einstein, il dit :"Voyez-vous celà! Je n'aurais jamais attendu de ce garçon une chose aussi brillante!"
|
Introduction de la conférence donnée par Minkowski en 1908 à Cologne:
"Les conceptions de l'espace et du temps que je veux développer devant vous ont surgi du sol de la Physique expérimentale et c'est ce qui fait leur force. Elles sont radicales. Désormais, l'espace en soi et le temps en soi ne sont plus que des ombres vaines et seule une sorte d'union des deux préservera une réalité indépendante.
![]() Cette vision de l'espace-temps permet de retrouver facilement le phénomène de dilatation des durées lorsqu'on passe d'un référentiel inertiel à un autre référentiel inertiel:
Cette vision de l'espace-temps permet de retrouver facilement le phénomène de dilatation des durées lorsqu'on passe d'un référentiel inertiel à un autre référentiel inertiel:

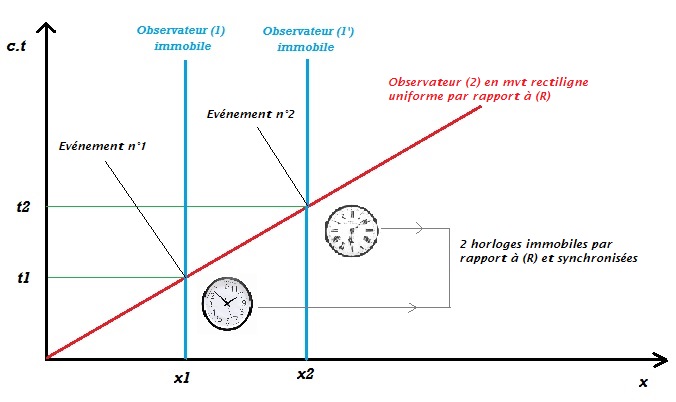
![]() Signalons également
que la transformation de Lorentz permettant de passer d'un système de
coordonnées à un autre lorsqu'on change de référentiel
galiléen, correspond en fait à une rotation du bloc "espace-temps"
défini par la métrique de Minkoswki. Or toute rotation entraîne
des effets de perspectives et c'est pourquoi les longueurs
semblent se contracter et les durées se dilater.
Signalons également
que la transformation de Lorentz permettant de passer d'un système de
coordonnées à un autre lorsqu'on change de référentiel
galiléen, correspond en fait à une rotation du bloc "espace-temps"
défini par la métrique de Minkoswki. Or toute rotation entraîne
des effets de perspectives et c'est pourquoi les longueurs
semblent se contracter et les durées se dilater.
Par définition, la pseudo-distance "ds" reste constante et on peut dès lors chercher les différents changements de coordonnées dans E4 laissant invariant "ds". Parmi les différentes isométries envisageables, il y a les translations dans l'espace et le temps, les rotations d'espace mais aussi les rotations d'espace-temps vu le caractère pseudo-euclidien de la métrique de Minkoswki. Cette dernière correspond en fait à un changement de référentiel galiléen comme on peut le constater:

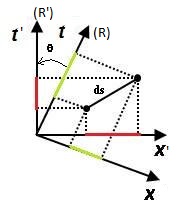
On peut remarquer que plus la vitesse est élevée, plus l'angle de rotation q devient important et plus l'effet de perspective est prononcé : contraction des longueurs et dilatation des durées sont davantage marquées.
4°) Une équation pour la célébrité
Revenons maintenant aux lois de la mécanique classique. Ces lois, ou plutôt les équations mathématiques traduisant ces lois, étaient bien invariantes sous une transformation de Galilée. Comme on l'a déjà expliqué, cette transformation n'est pas tout à fait correcte mais doit être remplacée par celle de Lorentz. Il faut donc modifier l'expression mathématique des lois de la mécanique et/ou les expressions de certaines grandeurs physiques intervenant dans ces équations (impulsion, énergie etc..) afin que celles-ci gardent bien la même forme après une transformation de Lorentz. Une analyse détaillée montre que l'expression de la seconde loi de Newton n'a pas à être modifiée mais qu'il faut par contre remanier les expressions mathématiques de l'impulsion et de l'énergie mais aussi admettre que la force n'est plus invariante lors d'un changement de référentiel galiléen.

On peut ensuite utiliser les équations de Hamilton pour en déduire les nouvelles expressions de l'impulsion et de l'énergie (dans le cas où la particule est libre).
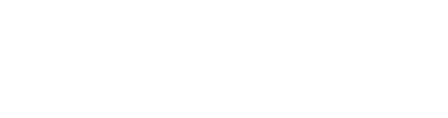 soit
soit
![]() (1)
(1)
Si la particule est libre:
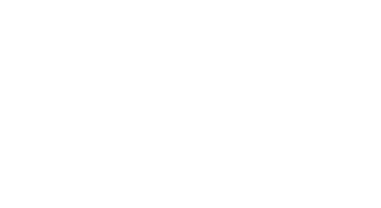 soit
soit
![]() (2)
(2)
On constate que d'après la relation (2) il faudrait fournir une quantité d'énergie infinie pour accélérer un corps de masse m jusqu'à la vitesse de la lumière ( car g tend vers l'infini lorsque v tend vers c ). En conclusion, tout corps matériel ne peut atteindre la vitesse de la lumière. En terme Newtonien, la masse inerte d'un corps (représentée par le terme " g.m ") augmente lorsque sa vitesse croit si bien que la résistance de ce corps à une augmentation de vitesse supplémentaire tend vers l'infini à l'approche de "c" et il n'est donc pas possible que ce corps puisse atteindre un jour la vitesse de la lumière .
|
|
Remarque : Pour une particule au repos, v = 0 donc g = 1 et par conséquent : E = m c 2 On retrouve ici la célèbre équation exprimant le fait que l'énergie peut correspondre à de la masse et la masse à de l'énergie. |
Une autre méthode (celle utilisée par Einstein) est de partir de l'expression de la force de Lorentz et de chercher dans un premier temps comment les champs E et B sont modifiés lors d 'une transformation de Lorentz lorsqu'on passe du référentiel R à R'.
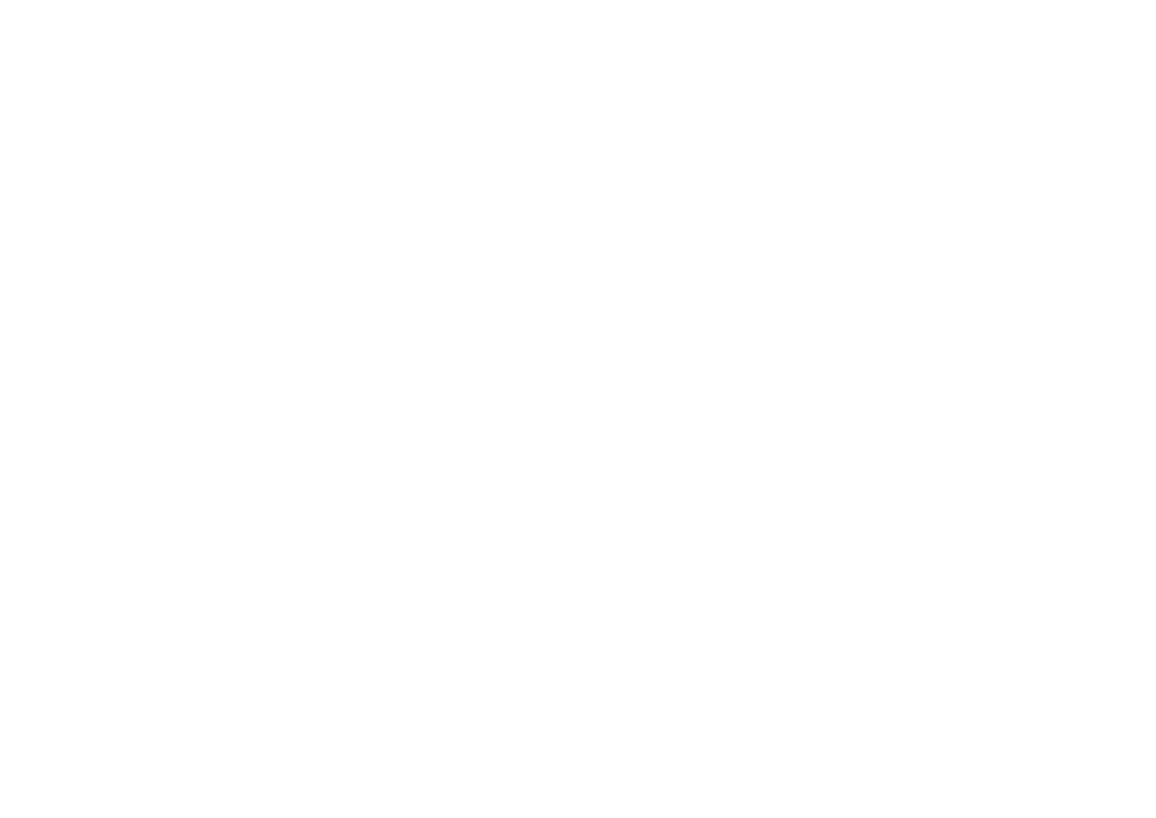
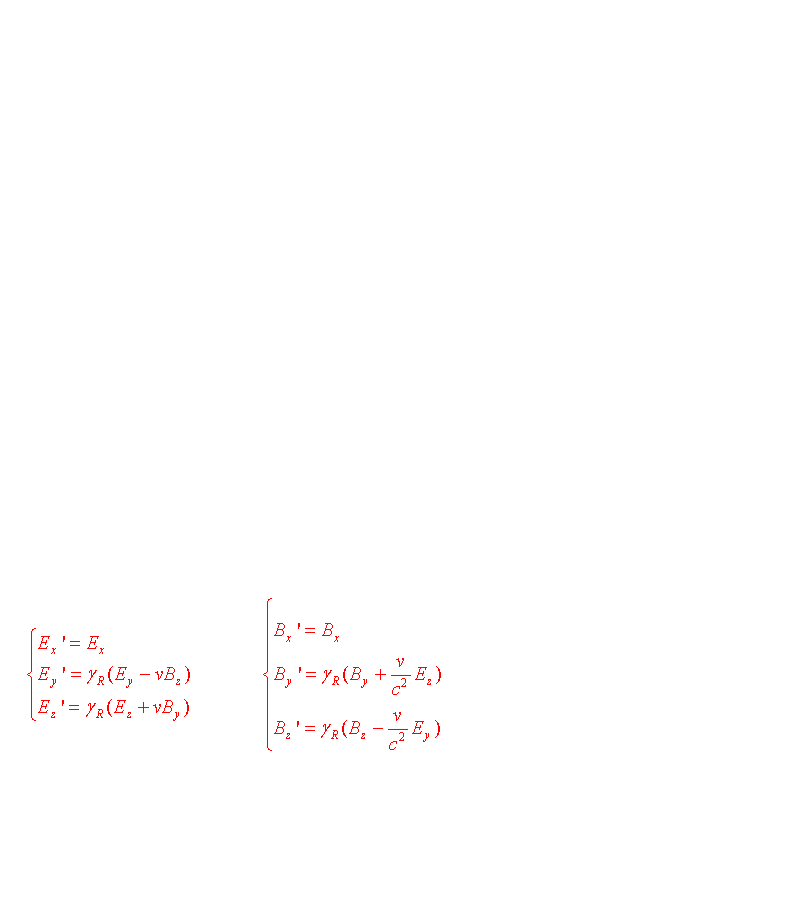
En comparant les 2 expressions, on vérifie aisément que la mécanique classique est bien une approximation de la théorie d'Einstein lorsque v << c
Dans un second temps , on étudie le mouvement d'une particule chargée plongée dans un champ électromagnétique en se plaçant dans 2 référentiels (R) et (R') animés l'un par rapport à l'autre d'un mouvement rectiligne et uniforme.
On établit l'équation du mouvement de cette particule dans le premier référentiel puis à l'aide des équations de transformation des champs et des accélérations, on obtient l'équation du mouvement de cette même particule dans le second référentiel. La covariance des lois physiques imposée par le principe de relativité permet ensuite de comparer les 2 équations qu'il faudra ensuite "ajuster" pour qu'elles gardent la même forme.

Ainsi en mécanique relativiste la loi du mouvement est bien la même qu'en mécanique classique mais il faut changer l'expression de la quantité de mouvement.
Pour l'expression de l'énergie, on utilise ensuite le théorème de l'énergie cinétique après avoir exprimé le vecteur dp/dt dans la base de Frenet:
(1) ![]()
(2) Théorème de l'Ec
:  d'où E = g.m c2
d'où E = g.m c2
5°) Un peu d'histoire pour n'oublier personne...
On attribue souvent la théorie de la relativité uniquement à A.Einstein. Même si cette théorie a été présentée pour la première fois de façon claire et simple par le jeune physicien (sans aucune référence aux travaux antérieurs de Lorentz et Poincaré alors qu'il semble indéniable qu'il en ait eu connaissance), Henri Poincaré avait dès 1902 compris lui aussi que les concepts de temps absolu et d'espace absolu étaient caduques comme il l'explique dans son livre "science et hypothèse". Il a été le premier a correctement formuler les transformations de Lorentz même si elles ne portent pas son nom, et à imaginer que l'interaction gravitationnelle se propageait à la vitesse de la lumière et non instantanément comme en théorie Newtonienne. Sans rien enlever au génie d'Einstein (déjà illustré par sa théorie de l'effet photoélectrique et du mouvement Brownien), on peut tout de même s'étonner que la théorie de la relativité restreinte ne soit pas davantage attachée au nom de Poincaré ...
|
Henri Poincaré, né le 29 avril 1854 à Nancy et décédé à Paris le 17 juillet 1912 , fut un mathématicien et physicien français. Artisan de génie, il est l'homme de l'ombre de la relativité générale : c'est lui qui le premier étudia les propriétés des espaces non euclidiens qui servirent plus tard à Albert Einstein pour établir la théorie de la relativité générale. Il est le cousin de l'homme politique et président de la France Raymond Poincaré. Il est l'inventeur de l'attracteur étrange, la solution à l'insoluble problème des trois corps : il trouva que trois corps obéissant à la gravitation universelle de Newton ont, sous certaines conditions, une trajectoire qui dépend fortement de la condition initiale. Ainsi, les pauvres humains que nous sommes ne pourront jamais déterminer avec exactitude le destin de ces corps car la moindre perturbation dans nos mesures entraînerait irremédiablement une forte différence de trajectoire. Ces supputations sont à l'origine de la théorie du chaos. Il fut aussi le dernier à avoir la double spécificité de comprendre l'ensemble des mathématiques de son époque et d'être en même temps philosophe. Il détient jusqu'à maintenant le record de la moyenne des notes obtenues au concours d'entrée à l'école polytechnique. Il rentra major, en sorti deuxième et intégra ensuite le corps des mines. Lorsque son professeur de mathématiques de "math spé" parlait de lui, il disait : " j'ai dans ma classe un monstre de mathématiques.." |