

![]()




1°) Le principe cosmologique ( cosmologie )
Formulé en 1917 par A.Einstein, le principe cosmologique stipule que l'univers est homogène (son apparence générale ne dépend pas de la position de l'observateur) et isotrope (son aspect ne dépend pas de la direction dans laquelle on l'observe) . Ainsi toute translation ou rotation de l'observateur ne doit pas changer la vision qu'il a de l'univers. Ce principe n'est valable qu'à grande échelle c'est à dire à des échelles supérieures à celles des amas de galaxies.
|
Univers homogène à grande échelle |
Univers hétérogène à petite échelle |
Le principe cosmologique est bien vérifié par les observations. La preuve la plus évidente en ce sens est l'isotropie quasi parfaite du fond diffus cosmologique qui correspond à "l'image" de l'univers tel qu'il était 380 000 ans après le big bang. Néanmoins, si l'univers était déjà si fortement homogène et isotrope à cette époque (de même qu'il l'est globalement resté durant les quelques 13 milliards d'années qui ont suivi), il reste à comprendre pourquoi une homogénéité quasi parfaite reignait déjà dès les premiers instants alors même que tous les points de l'espace constituant l'univers à cette époque ne pouvaient être causalement relié entre eux. Le modèle de l'inflation cosmique semble pouvoir répondre à cette question.
|
Carte de la sphère céleste montrant les fluctuations (ou anisotropie) du fond diffus cosmologique observées par le satellite WMAP puis Planck (seconde image) |
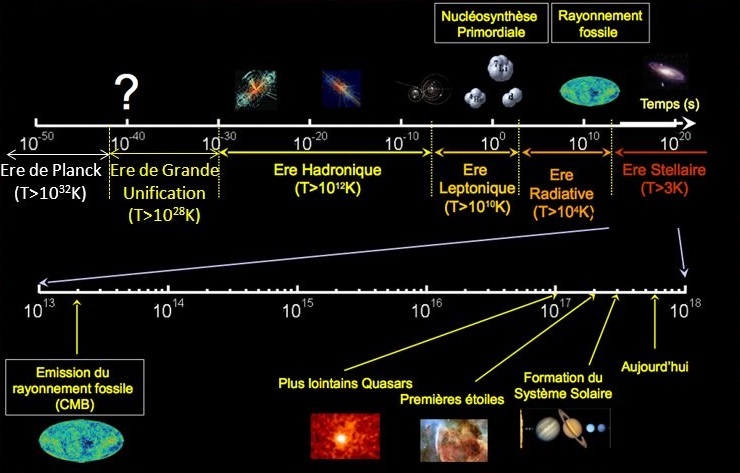
Découvert en 1965 par les 2 radioastronomes Penzias et Wilson, le fond diffus cosmologique est un rayonnement électromagnétique de type "corps noir" à la température de 2,7 °K. Le modèle cosmologique standard interprète ce rayonnement comme ayant été émis environ 380 000 ans après le big Bang lorsque l'univers, suffisamment refroidi en raison de son expansion, a permis à la lumière de se découpler de la matière. Une analyse minutieuse (par les satellites COBE, WMAP puis Planck) de ce rayonnement montre qu'il est presque parfaitement isotrope mis à part quelques infimes irrégularités très certainement à l'origine de la formation ultérieure des galaxies. |
|
Imaginé par A.Guth en 1979, l’inflation est un processus qui, dès les premiers instants, a permis de dilater les dimensions de l’univers de façon titanesque. Quelques 10-35 s après le « Big-Bang » et alors que la température de l’univers ne cessait de chuter, un champ de Higgs dénommé « inflaton » s’est retrouvé un court instant dans un état d’énergie qu’il n’aurait pas du avoir sans l’aide d’une fluctuation quantique appropriée. Cet état d’énergie qui correspond à ce qu’on appelle le « faux vide » a communiqué à l’univers une énorme poussé l’amenant à se dilater brusquement de façon exponentielle. Puis, une fois l’inflaton ayant repris son état d’énergie minimale qui correspond à ce qu’on appelle alors le « vrai vide », l’énergie du champ a servi à engendrer des particules. Une analogie souvent
citée est celle de l’eau en surfusion, c'est-à-dire de l’eau refroidie à moins
de 0°C sans geler. Au fur et à mesure que se poursuit le refroidissement, l’eau
finit pas geler soudainement et abandonne ensuite sa chaleur latente de fusion
dans le processus comme le fit l’univers lorsqu’il est passé du « faux
vide » au « vrai vide ».. Aujourd'hui, ce modèle a été abandonné car non conforme aux résultats obtenus par le satelitte "Planck"
|
Lorsque le rayonnement cosmologique a été émis 380 000 ans après le big-bang, seules les parties de l'univers séparées de 380 000 a.l (si on ne tient pas compte du phénomène d'expansion) pouvaient être reliées causalement ce qui signifie que le processus d'homogénéisation n'a pu se faire que sur des distances de 380 000 al au mieux. Le problème est que l'univers possède à cette période une taille déjà bien supérieure si bien que le fond diffus cosmologique n'a aucune raison d'être totalement homogène et isotrope comme le prouvent les différentes observations. La solution du problème est que toutes les régions de l'univers à cette époque étaient déjà en "contact" avant d'être écartelées par l'inflation. Ainsi, l'univers que nous observons est très uniforme aujourd'hui car il est le résultat de la dilatation extrême d'un germe minuscule dans lequel l'énergie avait déjà eu le temps d'être distribuée de façon uniforme.
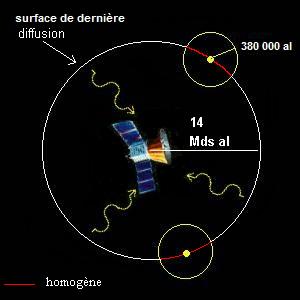
Chacun des points de la surface de
diffusion possède une sphère de causalité de 380 000 al au maximum.
Pourtant, le rayonnement issu de cette surface et que l’on observe aujourd’hui
est parfaitement isotrope !
L'inflation cosmologique permet également d'expliquer pourquoi l'univers semble être aussi plat aujourd'hui alors qu'il aurait pu adopter n'importe quelle autre forme. Quelque soit la courbure que possédait l'univers dès ses débuts, celle-ci a été littéralement "gommée" par l'inflation de la même manière que la courbure mesurée par un observateur situé sur la surface d'un ballon démesurément gonflé peut paraître nulle.
L'inflation prévoit ainsi un univers plat et donc une densité d'énergie totale égale à la densité d'énergie (massique) critique.
2°) Symétries spatiales et tenseur métrique
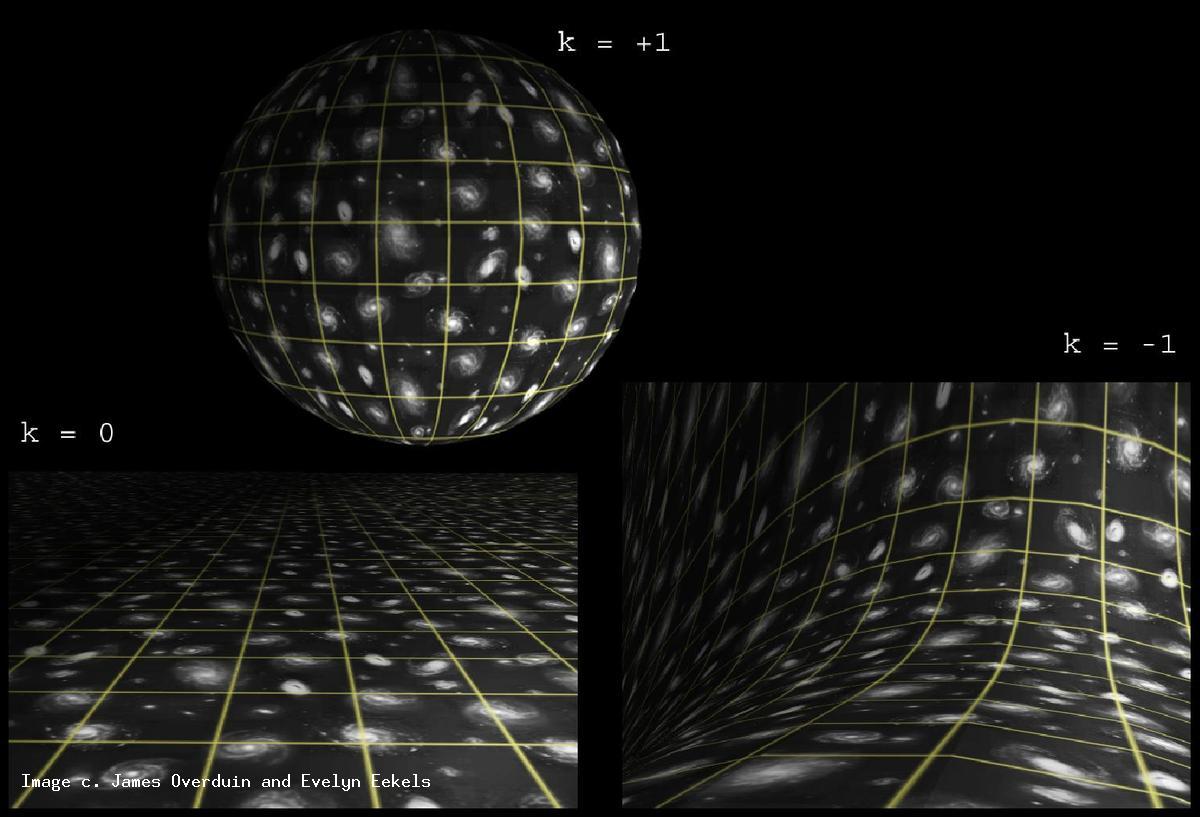
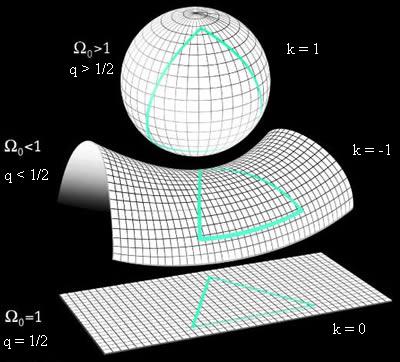
Le fait que notre univers soit homogène et isotrope restreint de façon drastique les formes géométriques que la partie spatiale de notre univers peut adopter. Les seules formes possibles pour l'espace qui sont compatibles avec la condition de symétrie entre tous les points et toutes les directions sont les espaces 3D à courbure constante, c'est à dire les espaces possédant une symétrie maximale. On peut montrer que seule la 3-sphère, la 3-hyperboloide et l'espace euclidien à 3 dimensions respectent les conditions de symétrie imposées par l'homogénéité et l'isotropie de l'univers.
a) La 3 sphère (courbure constante positive)
Une 3-sphère est l'analogue d'une sphère en dimension supérieure. C'est l'ensemble des points équidistants d'un point central fixé dans un espace euclidien à 4 dimensions.

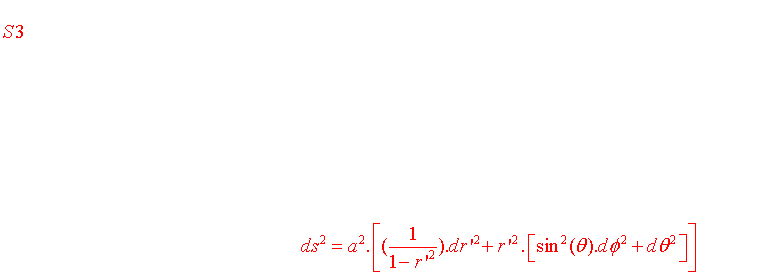
b) L'espace euclidien 3D (courbure nulle)
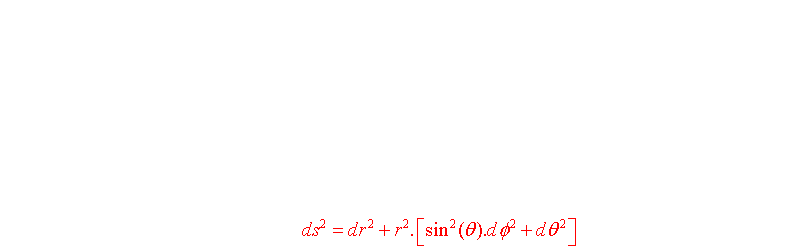

c) La 3 hyperboloide (courbure négative)
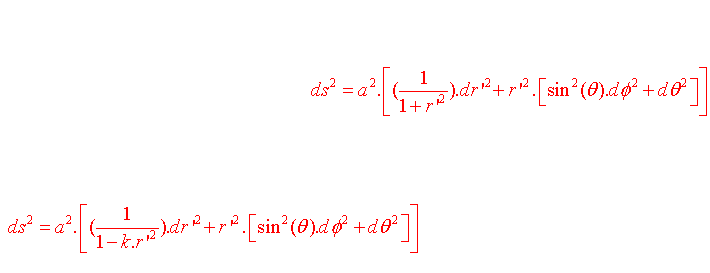
![]()
3-1) Une prédiction théorique
En 1917, la plupart des scientifiques étaient persuadés que l'univers se résumait à la voie lactée, un groupe stables d'étoiles. Certes, il se pouvait que certaines étoiles individuelles se déplaçaient à l'intérieur, mais en considérant la voie lactée toute entière, la caractéristique de l'univers semblaient bien être la stabilité. La voie lactée n'était ni très grande, ni très petite mais semblait être là depuis l'éternité selon les croyances de l'époque.
Grâce à sa toute dernière théorie achevée en 1915, A.Einstein essaya dès lors de décrire cet univers à l'aide d'un modèle théorique. Selon lui, l'univers devait être statique mais aussi fini (ressemblant à la surface d'une sphère) de telle sorte qu'il n'y ait pas de "bords", et devait contenir de la matière distribuée uniformément dans l'espace.
Etonnament, lorsqu'Einstein posa les équations décrivant un tel univers statique, elles indiquaient au contraire un univers soit en expansion soit en contraction ! Le seul moyen de le rendre immobile pour imiter l'apparence de la voie lactée était d'ajouter un terme supplémentaire aux équations de la RG: la fameuse constante cosmologique ![]()
3-2) La découverte de Hubble
Après de longues observations passées entre 1919 et 1924 derrière l'oculaire du grand télescope du Mont Wilson aux Etats-Unis , Edwin Hubble réussit à prouver, grâce à la méthode des céphéides, que les nébuleuses spirales que l'on croyait être situées dans la voie lactée, étaient en réalité de véritables galaxies situées bien au delà de la notre et qui plus est, étaient réparties de façon uniforme dans ses grandes lignes.
|
Edwin Hubble (1889-1953) |
Malgré cette découverte capitale, les travaux de Hubble ne s'arrêtèrent
pourtant pas là; Grâce aux nombreuses mesures de décalages Doppler déjà
effectuées par l'astronome Slipher, il réalisa
que non seulement quasiment tous les décalages spectrales étaient orientés vers
le rouge (les galaxies s'éloignent) mais aussi que plus les galaxies étaient
petites et plus leur décalage vers le rouge semblaient importants. En supposant que toutes les galaxies ont plus ou moins la même
taille, cela signifiait que les plus petites galaxies n'étaient petites qu'en
apparence parce que plus éloignées et que grande distance et grande vitesse de
récession allaient de pair. Lorsque Hubble plaça sur un graphique la vitesse de récession des
galaxies en fonction de leur distance, il constata que les points étaient
sensiblement alignés et établit ainsi en 1929 ce qu'on appelle aujourd'hui la
loi de Hubble: v= H.r et qui signifie que plus une galaxie est éloignée et plus
sa vitesse de fuite est importante. En d'autres termes, Hubble venait de
découvrir que l'univers dans son ensemble était en expansion. (Bien que passé complètement
inaperçu à l'époque, l'abbé Georges Lemaître avait déjà montré en 1929 et à
l'aide des équations de la RG, que dans un univers en expansion, les galaxies
lointaines apparaîtraient se fuir avec des vitesses proportionnelles à leur
distance)
|
|
Il est important de préciser que les mesures obtenus par E.Hubble étant réalisées depuis la Terre, il serait logique de conclure que les galaxies s'éloignent seulement relativement à nous et ce de façon d'autant plus rapide qu'elles sont situées loin de la Terre. En fait, les décalages vers le rouge donnent une mesure de la vitesse à laquelle les galaxies se séparent les unes des autres et pas seulement par rapport à nous Terriens. En effet, nous ne sommes pas situés à un endroit particulier, le centre de l'univers. C'est donc l'espace tout entier qui est en expansion de telle sorte que n'importe quel autre observateur vivant ailleurs dans l'univers verrait exactement le même phénomène de récession. Une analogie souvent utilisée pour expliquer ce que signifie un univers en expansion est le ballon que l'on gonfle: n'importe quelle tâche dessinée sur la surface du ballon voit les autres tâches s'éloigner d'elle de la même façon, c'est à dire suivant la même loi: la loi de Hubble.
|
|
3-3) La métrique spatio-temporelle de Fridmann-Lemaître-Walker
°a) Partie spatiale de la métrique
Bien que l'espace soit en expansion, la symétrie reste toujours de mise. Quelque soit la galaxie dans laquelle on se situe, toutes les autres s'éloignent d'elle de la même manière selon la loi de Hubble. Autrement dit, même si l'univers change avec le temps, alors quelque soit sa position, chaque observateur entrainé avec l'espace qui se dilate, verra toujours autour de lui une tranche d'espace homogène et isotrope . La métrique de la partie spatiale sera donc toujours un espace à symétrie maximale mais dont le paramètre "a" (qui représente par exemple le rayon de l'hypersphère dans le cas de l'espace à courbure constante positive) sera fonction du temps.
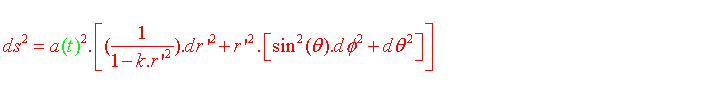
Par contre, à la différence d'un univers statique, les coordonnées ![]() représentent maintenant ce qu'on appelle les coordonnées comobiles, c'est à dire les coordonnées d'un
point M par rapport à un repère en réalité fixe dans l'espace mais mobile puisque lié à un espace qui se dilate (à la manière d'une toile élastique que l'on étire).
représentent maintenant ce qu'on appelle les coordonnées comobiles, c'est à dire les coordonnées d'un
point M par rapport à un repère en réalité fixe dans l'espace mais mobile puisque lié à un espace qui se dilate (à la manière d'une toile élastique que l'on étire).
Autrement dit, un point M immobile (représentant par exemple une galaxie quelconque dont on néglige le mouvement propre) aura toujours les mêmes coordonnées dans un tel repère bien que l'espace se dilate au cours du temps. (Bien que globalement immobiles dans l'espace, les galaxies s'écartent les unes des autres uniquement en raison de la dilatation de l'espace lui même). La comobilité, c'est donc l'immobilité au sein d'un espace qui est mobile.
Par exemple, par
rapport à un repère cartésien, cela signifie que ce sont les graduations des
axes qui s’étirent en même temps que l’espace de telle façon que les
coordonnées du point M restent les mêmes au cours du temps (si toutefois on
suppose bien sûr que le point M reste immobile relativement à l’espace)
a(t) est appelé "facteur d'échelle" ou encore "rayon d'univers"
r' est la coordonnée radiale comobile (indépendante du temps). Si l'espace est plat, elle représente la distance radiale comobile entre 2 points de l'espace.
r(t) = a(t).r' représente la distance géométrique c'est à dire la véritable distance séparant 2 points au cours du temps (dans le cas d'un espace plat).
b) Partie temporelle de la métrique
Le paramètre "t" doit-il dépendre de la position de l'observateur dans l'espace ?
L'évolution homogène de l'univers signifie que des horloges situées ici sur Terre, dans la galaxie d'Andromède ou ailleurs dans n'importe quelle autre galaxie seront toutes, en moyenne, soumises à des conditions physiques similaires et égreneront donc le temps à peu près de la même façon. L'homogénéité et l'isotropie de l'espace, bien qu'en expansion , garantit ainsi une synchronie cosmique: le temps s'écoule sensiblement de façon uniforme partout dans l'univers.
Le paramètre "t" représente ainsi le temps comobile c'est à dire le temps propre: il s'agit du temps mesuré par des horloges stationnaires par rapport à l'espace lui même. Toutes ces horloges sont en moyenne synchronisées et mesurent globalement le temps écoulé depuis le "Big-Bang": on lui donne le nom de "temps cosmologique"
Mathématiquement parlant, la partie temporelle de la métrique, représentée par le terme g00 , doit être indépendante de notre position dans l'espace: il prend par convention la valeur "1" comme dans le cas de l'espace-temps vide de Minkowski.
c) La métrqie de FLRW
En définitive la métrique de l'espace-temps sensée représenter notre univers sera de la forme:
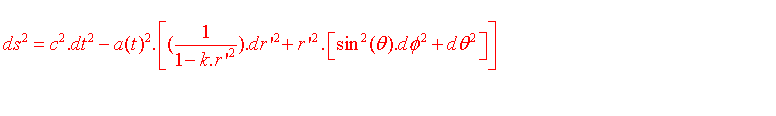

4°) Les équations de Friedmann
A partir de la métrique de FLRW:



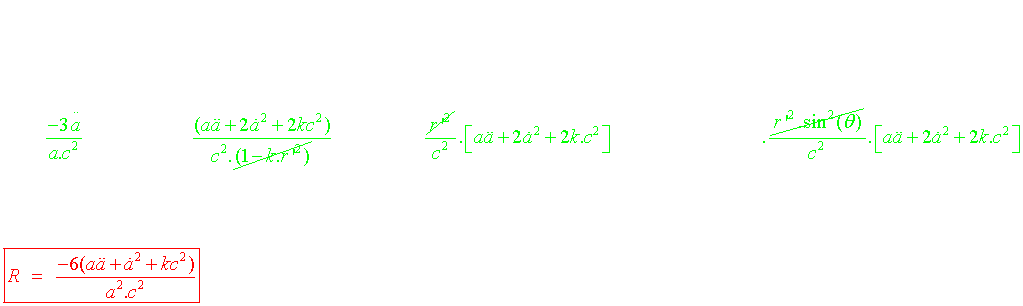
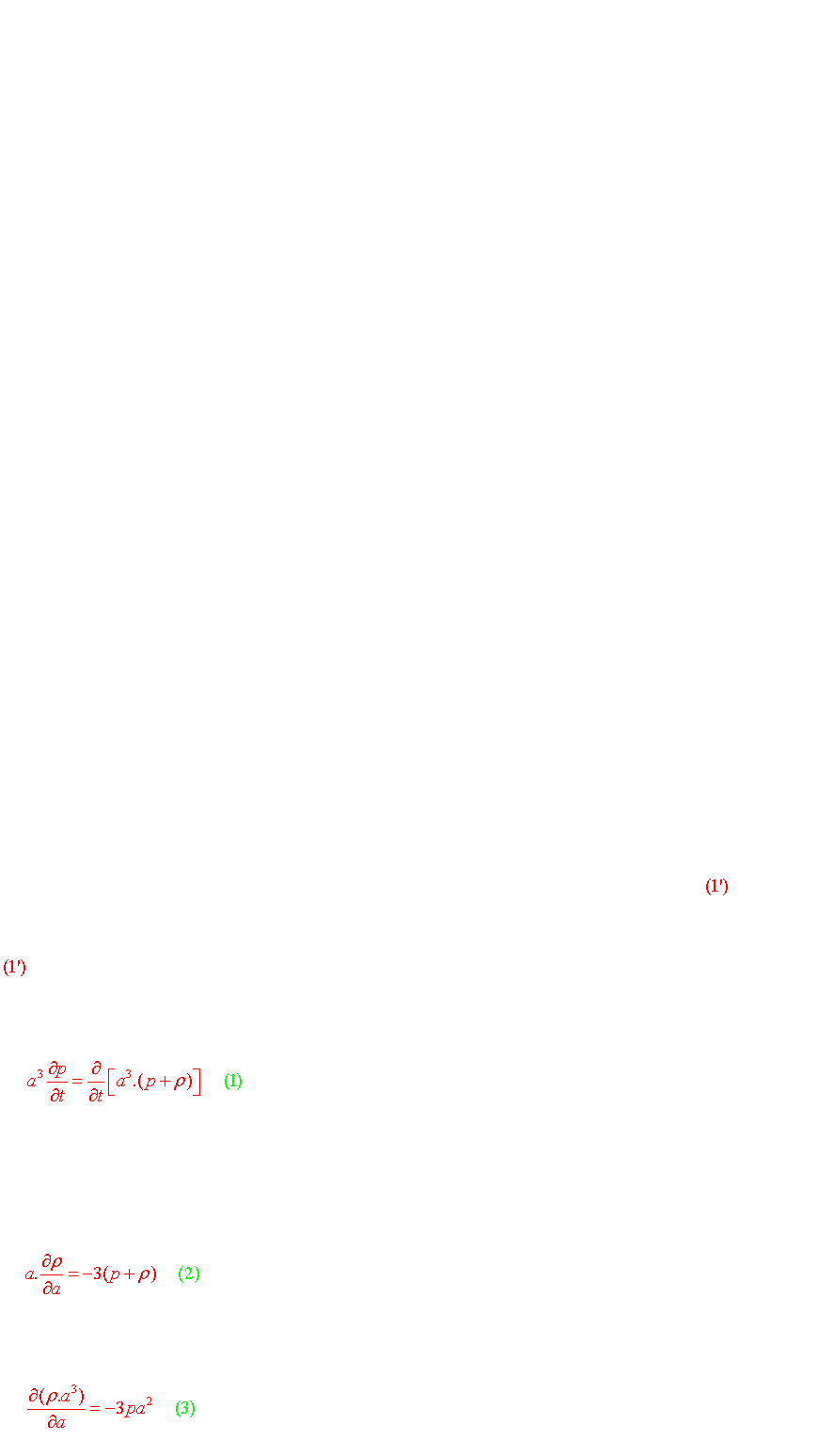
![]()


5°) Les différents modèles d'univers (uniquement les espaces topologiques simplement connexes)
![]() 5-1) Le modèle d'Einstein (1917)
5-1) Le modèle d'Einstein (1917)
Comme la plupart des scientifiques de l'époque, Einstein considère que l'univers est globalement statique et homogène. Il l'imagine également fermé principalement pour des raisons liées au principe de Mach auquel il croit beaucoup. Il construit ainsi un modèle d'univers sphérique capable de rendre compte de l'essentiel des conditions phyiques qu'il pense devoir respecter.
Pourtant, il constate rapidement que ses équations n'admettent pas de solutions statiques et c'est ainsi pour satisfaire ce qu'il considère comme une exigence expérimentale (univers immobile) qu'il se trouve contraint de modifier légèrement ses équations en y ajoutant un terme supplémentaire : la constante cosmologique.
Cette constante se comporte comme une force répulsive permettant de contrebalancer exactement la force gravitationnelle attractive due à la matière, l'ensemble pouvant désormais tenir en équilibre.
La densité d'énergie r de l'univers détermine la taille de celui-ci qui fixe à son tour la valeur que doit prendre la constante cosmologique pour que l'univers soit statique.
![]() 5-2) Le modèle de De Sitter (1917)
5-2) Le modèle de De Sitter (1917)
Il s'agit d'un univers vide de matière mais avec une constante cosmologique non nulle. En raison de l'isotropie de l'espace, la métrique est de la forme:
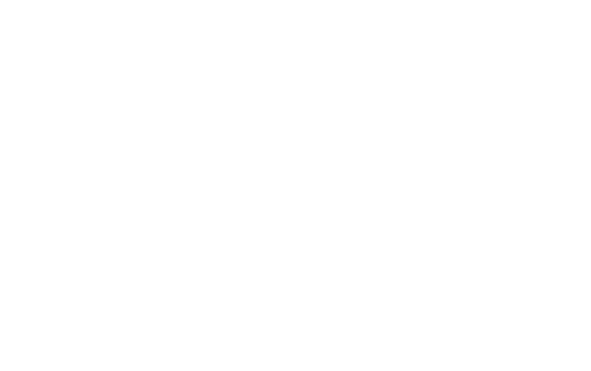

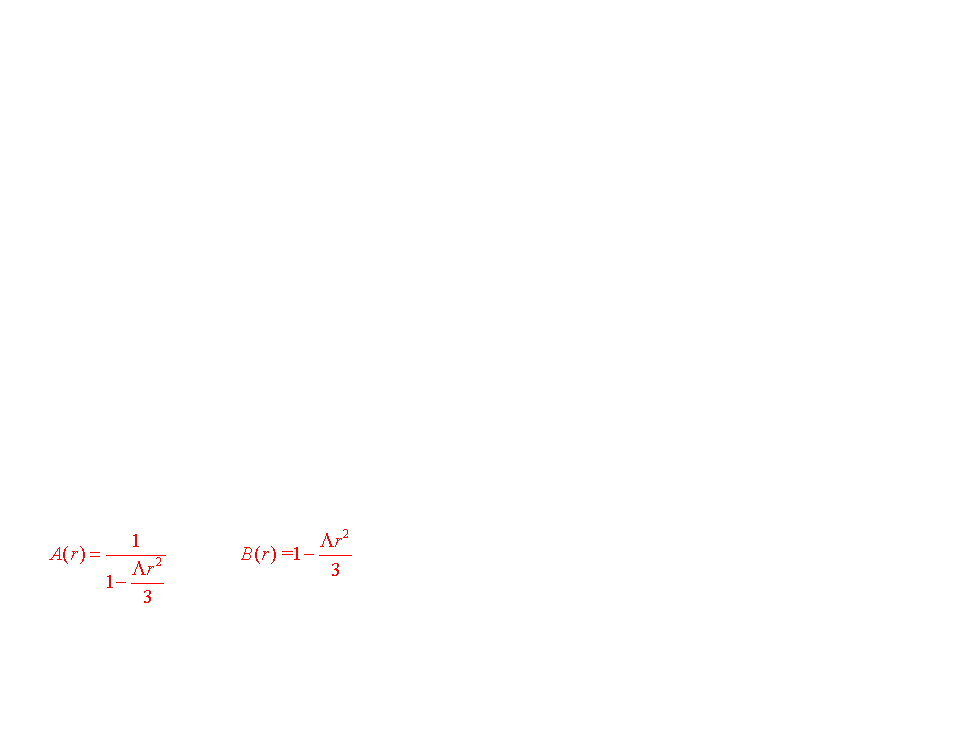
Le modèle d’univers de De Sitter n’est statique qu’en apparence en raison du système de coordonnées particulier qui a été utilisé. Comme l'a montré H.Weyl en 1923, il suffit par exemple d’introduire un peu de matière dans le modèle pour constater qu’elle tend à s’écarter de façon exponentielle. En 1925, G.Lemaître montre comment on peut introduire de nouvelles coordonnées qui rendent la métrique de "De Sitter "non statique et démontre qu'il existe alors une relation linéaire entre la vitesse et la distance.
Un univers vide avec constante cosmologique ne peut donc pas être statique.
![]() 5-3) Les modèles de Friedmann (1922-1924)
5-3) Les modèles de Friedmann (1922-1924)
Dans cette catégorie de modèles d’univers, le fluide cosmique, principalement constitué des galaxies, est assimilé à un gaz parfait (les interactions entre galaxies sont négligées) dont la pression est négligeable (l’énergie « d’agitation thermique » des galaxies est négligeable devant leur énergie de masse).
Bien qu' A. Friedmann ait traité les situations avec une constante cosmologique , on se limitera ici aux cas paticuliers où![]() = 0
= 0
Tous les modèles de Friedmann possèdent une singularité dans le passé et qui correspond à ce qu’on appelle communément le « Big Bang ».


Par exemple, selon la théorie de la gravitation quantique à boucles, (théorie visant à quantifier la gravitation) le big bang n'est qu'une étape dans l'histoire de notre univers et non "l'instant" de la création "ex-nihilo" de celui-ci. Imaginer d'ailleurs que notre univers puisse surgir spontanément du néant pose de sérieux problèmes..Comment peut-on passer de rien à quelque chose ?
En effet, selon cette théorie, les équations de Friedmann sont légèrement modifiées et notamment l'équation (4) qui s'écrit désormais:
En gravitation quantique à boucles, l'espace temps est constitué "d'atomes" d'espace-temps dont les dimensions caractéristiques sont de l'ordre de la longueur de Planck. En terme de densité d'énergie, cela signifie que la densité d'énergie maximale d'un quanta d'espace-temps ne peut pas dépasser la densité d'énergie de Planck dont la valeur vaut 4.635 10113 J/m3
Près du big-bang, la densité d'énergie devient très élevée et approche la densité de Planck; Le terme de droite s'annule tout comme la dérivée de a(t). Il n'y a dès lors plus de contraction, ni d'expansion et la densité d'énergie ne peut plus croître au delà de la densité de Planck. Tout se passe comme si il existait une force répulsive empêchant l'univers de devenir trop petit pour finir sur une singularité.
A cause de cette force répulsive à très petite distance, un univers en contraction va violemment rebondir et passer à une phase d'expansion. La théorie indique ainsi que "l'explosion" initiale de notre univers, le big-bang, pourrait être le résultat d'un gigantesque rebondissement cosmique, un big-bounce, consécutif à la contraction cosmique d'un univers similaire au nôtre. Dans ce type de théorie, nul besoin de faire intervenir un champ scalaire de type "inflaton" pour expliquer une phase d'expansion rapide juste après le big-bang.
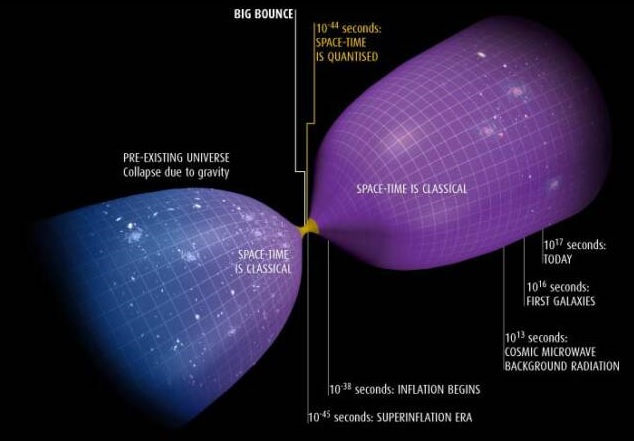
Avant d'expliciter les différentes solutions des équations de Friedmann, on introduit au préalable les paramètres cosmologiques:
Remarque: la relation de Hubble v= Ho.r n'est qu'une approximation seulement valable pour des galaxies dont la vitesse de récession est modérée.
En effet lorsqu'on regarde une galaxie située par exemple à 2 millions d'année-lumière, on mesure aujourd'hui la vitesse et la distance à laquelle se situait cette galaxie il y a 2 millions d'années de là, c'est à dire le temps qu'il a fallu à la lumière pour parvenir de la galaxie jusqu'à nous. Si ce laps de temps est faible relativement au temps cosmologique, le taux d'expansion de l'univers mesuré par la "constante" de Hubble H n'a pas eu le "temps" de varier de façon notable et on peut ainsi considérer que sa valeur est sensiblement la même aujourd'hui.
Il en est de même pour la distance et la vitesse de récession de la galaxie étudiée: la distance et la vitesse que possédait la galaxie il y a 2 millions d'années ont quasiment les mêmes valeurs qu'aujourd'hui.
La relation ![]() n'est donc valable que si l'on considère des galaxies dont la vitesse de récession n'est pas trop élevée c'est à dire pour des galaxies modérément éloignées.
n'est donc valable que si l'on considère des galaxies dont la vitesse de récession n'est pas trop élevée c'est à dire pour des galaxies modérément éloignées.
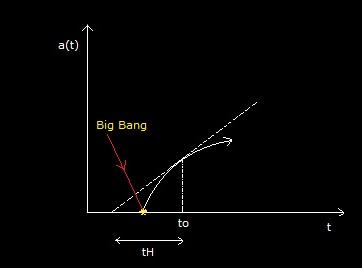
La connaissance de H0
permet d’évaluer l’âge de l’univers. En effet, si on considère que les galaxies
s’éloignent les unes des autres à vitesse constante (ce qui n'est pas le cas en réalité) alors la distance « r »
qui sépare 2 galaxies maintenant vaut r =v.tH ou tH représente
le temps écoulé depuis le Big-Bang. (tH est
aussi appelé "temps de Hubble")
Comme:

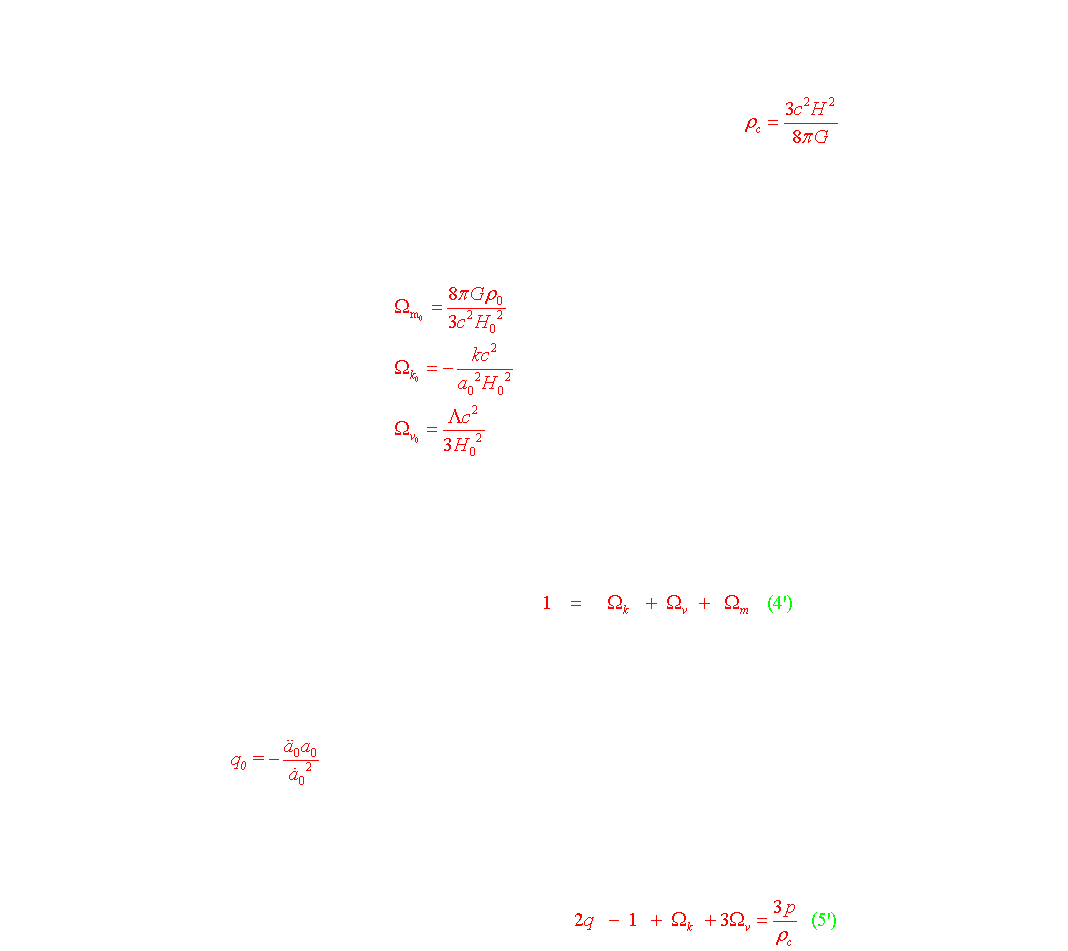
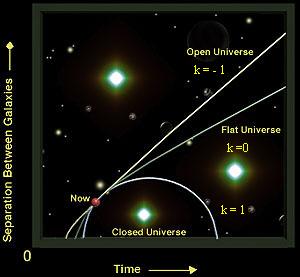
a) Le modèle d'Einstein-De Sitter (1932) (k=0)
Proposé conjointement par Einstein et De Sitter en 1932, il s'agit d'un cas particulier des modèles de Friedmann pour lequel l'espace 3D est supposé euclidien (k=0)a)
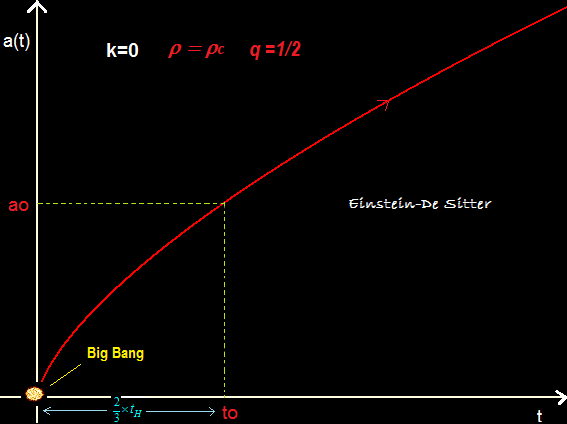
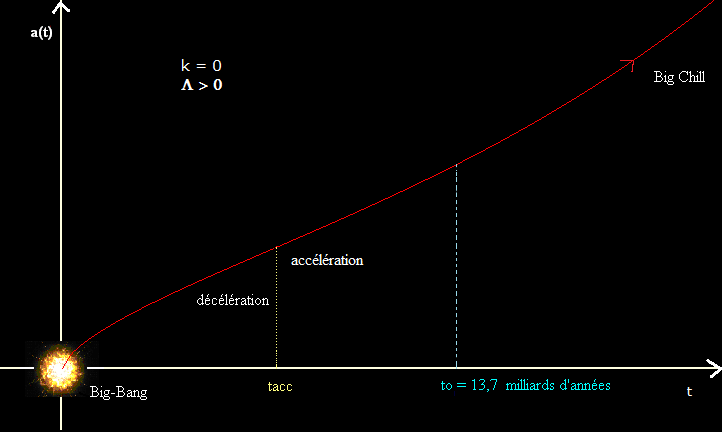
Il s'agit d'un univers ouvert dont l'expansion s'arrêtera au bout d'un temps infini.
Historiquement, ce modèle d'univers a été abandonné car en contradiction avec l'âge de certaines vieilles étoiles dont on estime la durée de vie supérieure à 10 -12 milliards d'années.
b) Le modèle sphérique (k=1) (1922)
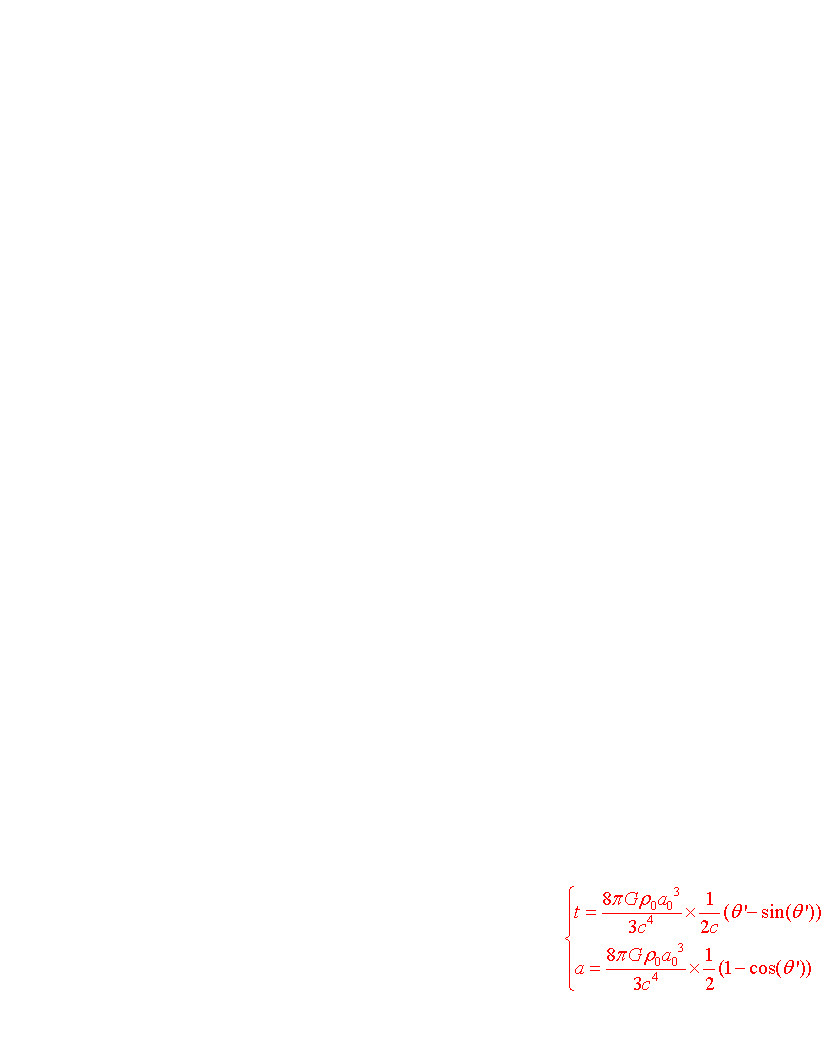
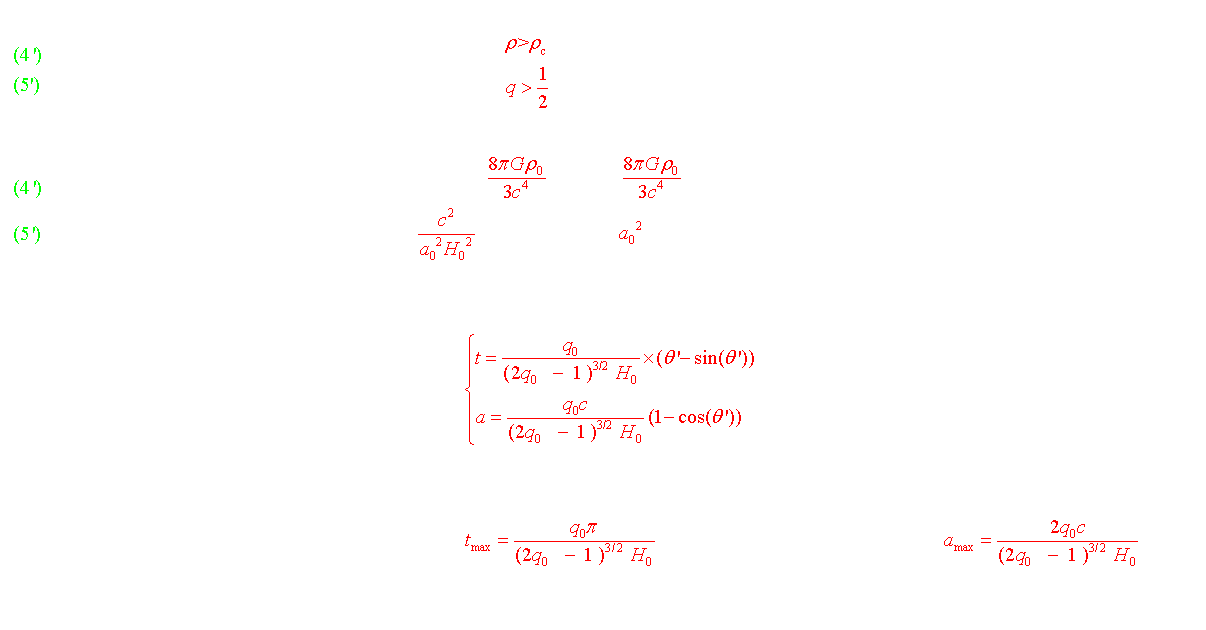
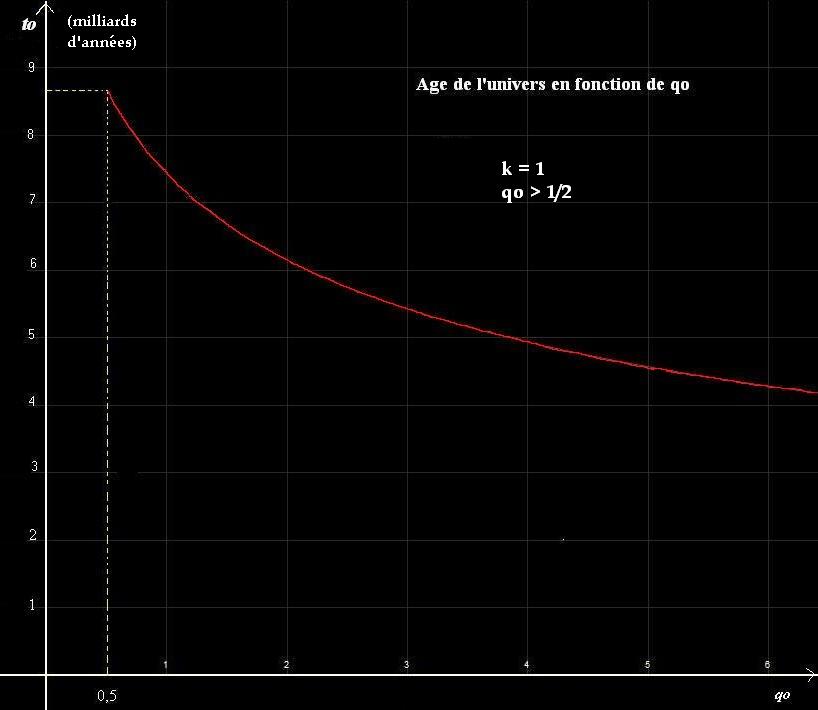
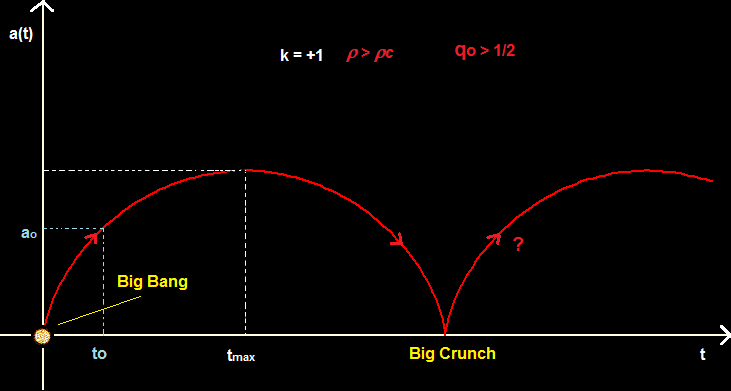
Conclusion : si r >rc l'univers est fini dans l'espace et dans le temps puisqu'il se termine inévitablement par un Big Crunch. Ce type d'univers a été abandonné car son âge actuel maximale est toujours plus petit que l'âge de certaines étoiles.
c) Le modèle hyperbolique (k=-1) (1924)

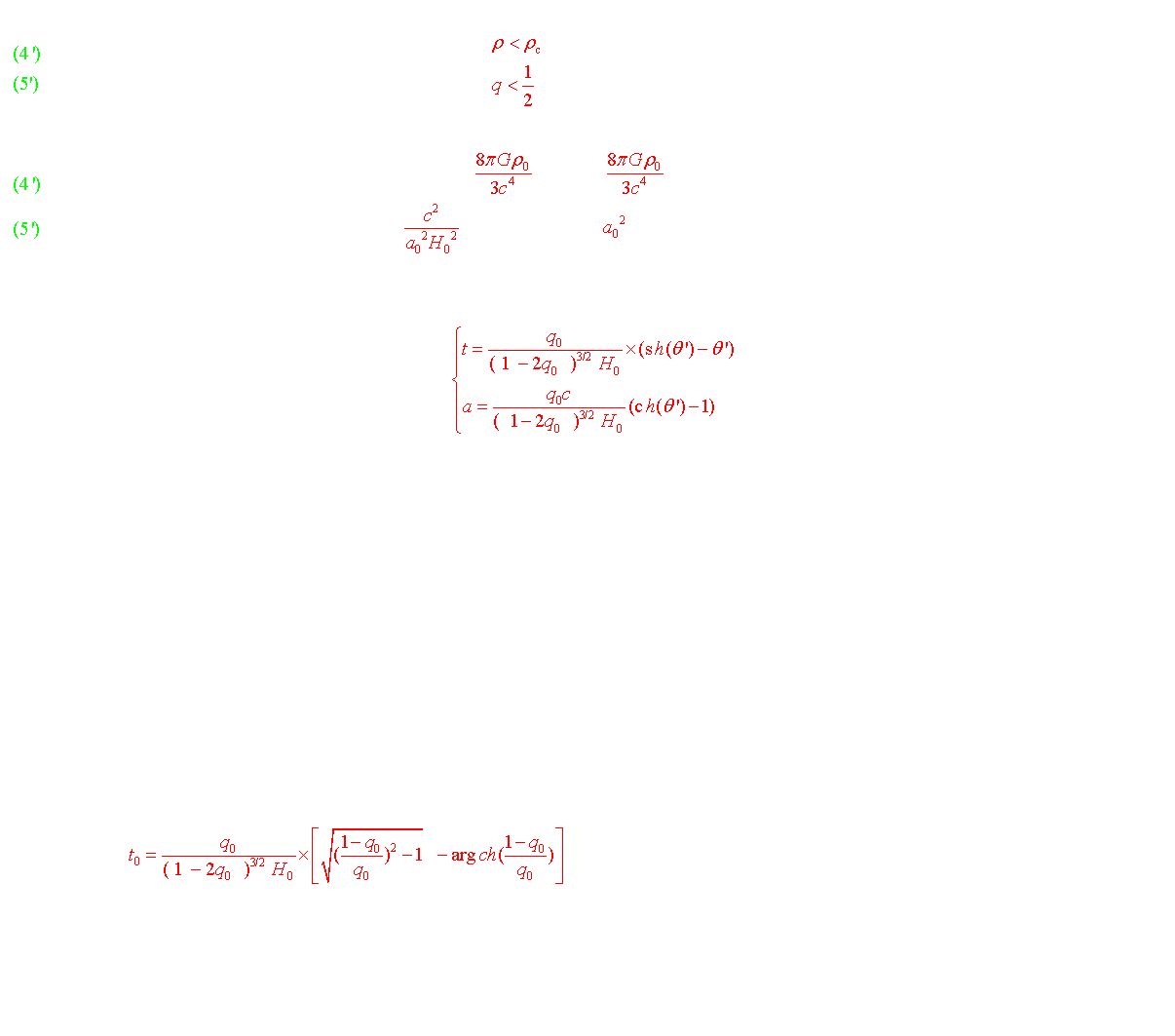
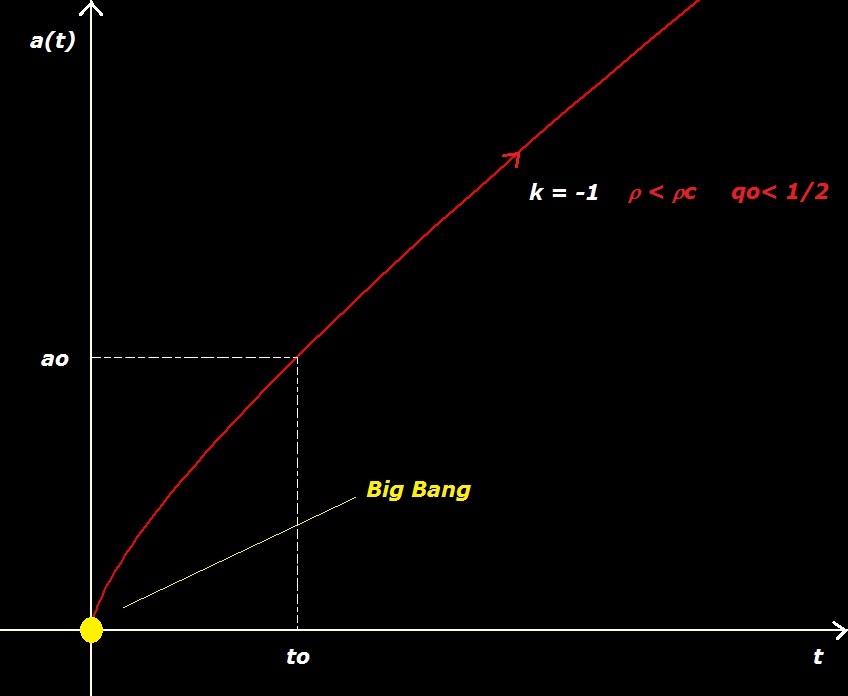
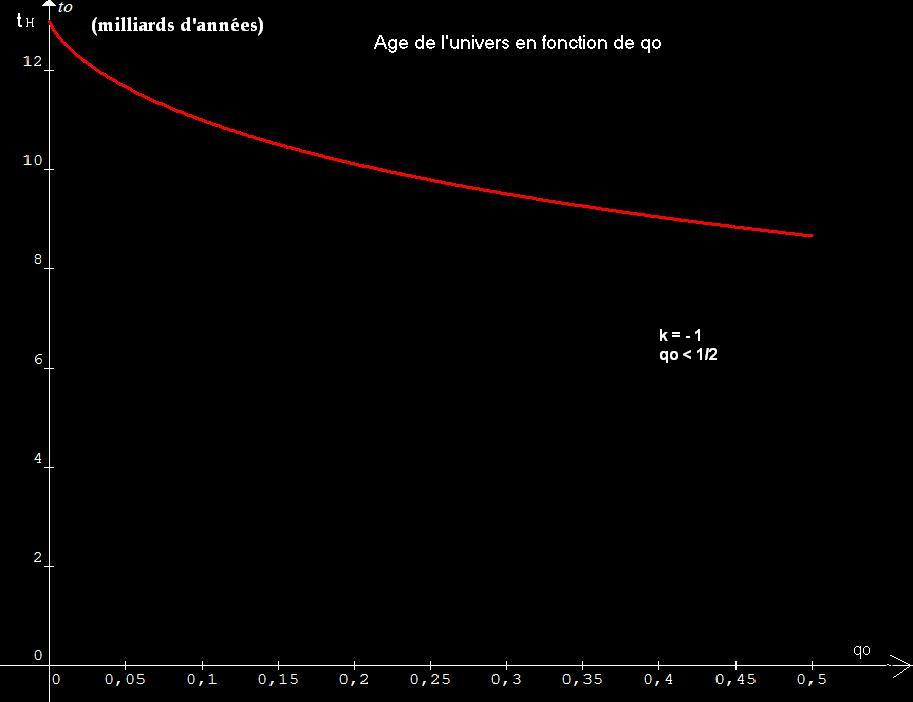
Conclusion : si r <rc l'univers est ouvert dans l'espace et dans le temps.
Avec un paramètre de décélération très faible, l'âge de l'univers reste compatible avec l'âge des plus vielles étoiles mais est en contradiction avec la valeur du paramètre de décélération que l'on mesure aujourd'hui à savoir qo < 0
Synthèse des modèles de Friedmann
![]() 5-4) Les modèles de Lemaître (1927-1931)
5-4) Les modèles de Lemaître (1927-1931)
Indépendamment et contrairement à Friedmann, les solutions proposées par G.Lemaître incluent non seulement la constante cosmologique mais aussi un terme de pression et sont donc plus générales que les modèles présentés par le physicien russe entre 1922 et 1924.
a) Le modèle de l'univers "jeune"
Le terme de pression prend toute son importance lorsque l’univers est jeune et que la pression dûe aux photons ne peut plus être négligée devant la densité d’énergie de la matière. Dans les premiers stades de l’univers, on peut même négliger les termes de densité d'énergie de matière et du vide par rapport à la pression de radiation.
En fait, l’approximation p = 0 n’est valable que pour les temps cosmologiques postérieurs à environ 90 000 ans (voir égalité matière-rayonnement un peu plus bas).
L'égalité matière-rayonnement :
Ainsi, pour t < 90 000 ans, l'évolution de univers est principalement régit par le rayonnement.
b) Les modèles d'univers avec constante cosmologique non nulle et pression négligeable.
b-1) Univers de courbure nulle (k=0) : Le modèle LCDM (lambda cold dark matter)
D’après les dernières mesures obtenues en étudiant les « supernovae » de type Ia, ainsi que ceux obtenus grâce au satellitte "Planck", il s’agirait du modèle le mieux adapté à l’univers observable. En effet, les dernières observations tendent à montrer que notre univers est plutôt « plat » et que son expansion s’accélère ce qui peut s’expliquer en faisant à nouveau intervenir une constante cosmologique positive.
Cette constante peut être incorporée dans le tenseur énergie-impulsion en rajoutant à celui-ci un terme supplémentaire que l’on peut interpréter comme étant le tenseur énergie-impulsion du vide et dont l’effet répulsif finirait par l’emporter lorsque l’univers serait devenu suffisamment grand.
L'origine véritable de cette énergie du vide, aussi appelée "énergie noire", n'est toujours pas comprise aujourd'hui. Les équations du modèle standard des particules permettent de calculer la valeur de la densité d'énergie du vide quantique mais le résultat le plus optimiste (ie tenant compte des théorie de supersymétrie) est toujours plus grand d'un facteur 1060 par rapport à la valeur mesurée expérimentalement. Il se pourrait aussi que la "constante" cosmologique responsable de l'accélération de l'expansion de l'univers trouve ses racines dans un champ scalaire issu des théories "tenseurs-scalaires", mais auquel cas la constante cosmologique n'en est plus vraiment une puisqu'elle serait dès lors susceptible de varier dans le temps et/ou l'espace...Pour le moment, les différentes expériences tendent à montrer que la fameuse constante d'Einstein semble effectivement se comporter comme une vraie constante.... le mystère reste donc entier !

Quelques explications quant à la notion de pression "négative"
Prenons par exemple un fil élastique. Il possède une pression négative parce que vous devez exercer un effort pour le tendre. Pour une substance de pression positive, comme l'air, c'est le contraire : vous devez exercer un effort pour le comprimer. Une pression positive génère une gravité attractive et donc une pression négative déclenche une gravité répulsive !
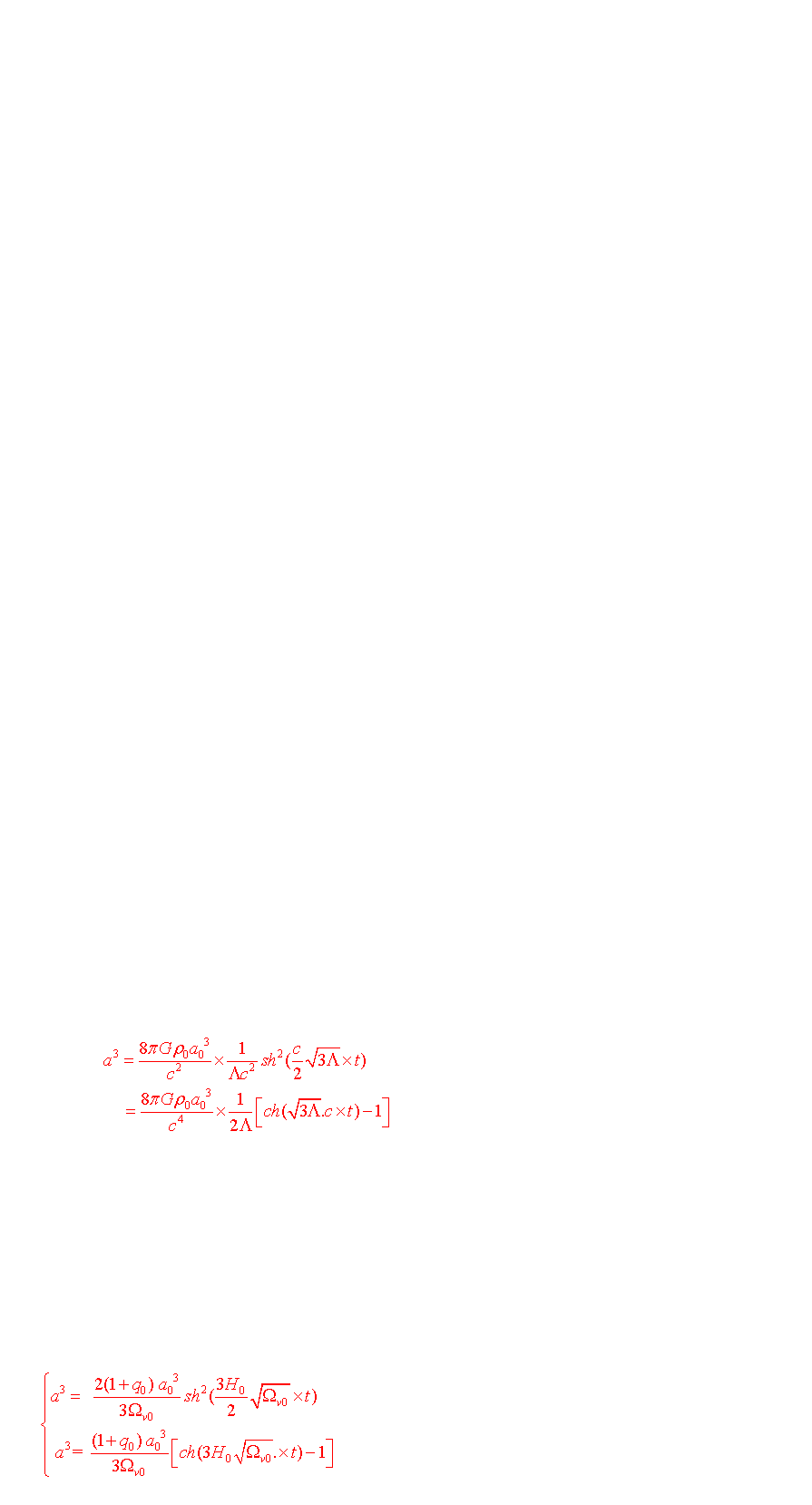


Age de la recombinaison : (âge pour lequel la température n'est plus suffisante pour ioniser les atomes d'hydrogène: l'univers commence à devenir transparent)-voir équation de Saha-
Une fois les photons découplés de la matière, ils n'intéragiront presque plus avec celle-ci et bien que l'équilibre thermique soit rompu, leur distribution énergétique restera celle de Bose-Einstein.
La température du rayonnement obéira donc toujours à la loi: a.T=cste
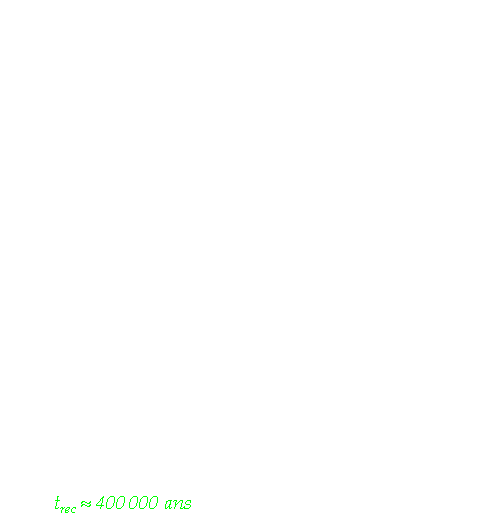
Il s'agit là d'une valeur approximative étant donné que l'on a négligé pour le calcul la densité d'énergie du rayonnement. Or il se trouve que juste après la recombinaison, celle-ci n'est pas encore négligeable bien que l'on soit entré dans l'ère de la matière. Un calcul plus réaliste donne t(rec) = 380 000 ans
L'horizon cosmologique
Il s'agit de la distance au-delà de
laquelle l'univers n'est plus observable car toute information sur cette partie
de l'univers n'a pas eu le temps de nous parvenir. Etant donné qu'aucune
information ne peut voyager plus vite que la lumière et que l’univers est âgé d’environ
13,7 milliards d’années, tout objet situé au-delà de 13,7 milliards d’années-lumière ne peut être observé. Néanmoins l’univers étant en expansion, la
distance réelle qui nous sépare de l’horizon cosmologique est supérieur à cette valeur.
Aujourd’hui, les seules informations que l’on peut obtenir de l’univers se font grâce à la lumière et celle-ci n’a pu voyager librement qu’environ 380 000 ans après le big-bang lorsque l’univers est enfin devenu « transparent ». La distance à laquelle se situe l'horizon cosmologique correspond donc à la distance qui nous sépare de la "surface de dernière diffusion".

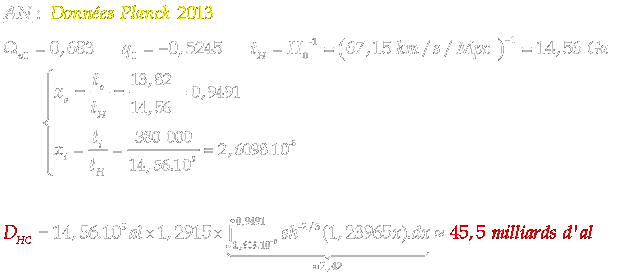
b-2) Univers de courbure positive (k= 1)
Il n'existe pas de solutions exactes aux équations de Friedmann dans ce cas, mais un traitement numérique permet de tracer les courbes a=f(t) à l'aide d'un logiciel.
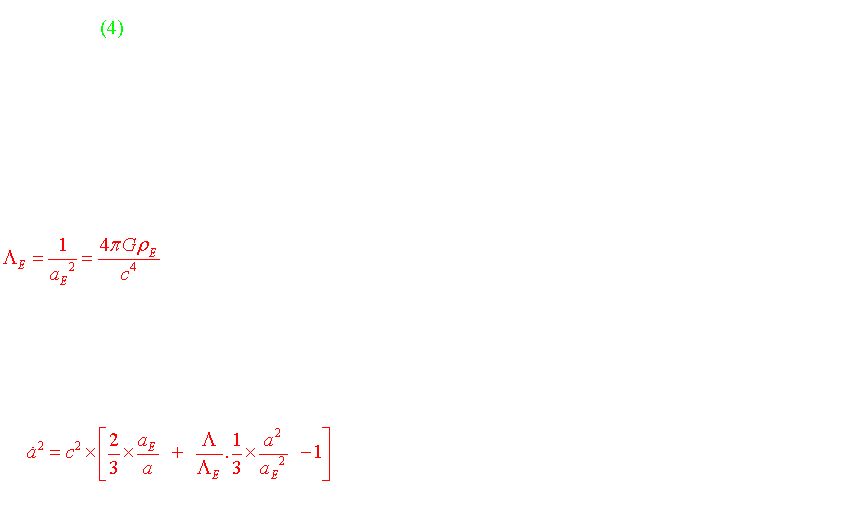
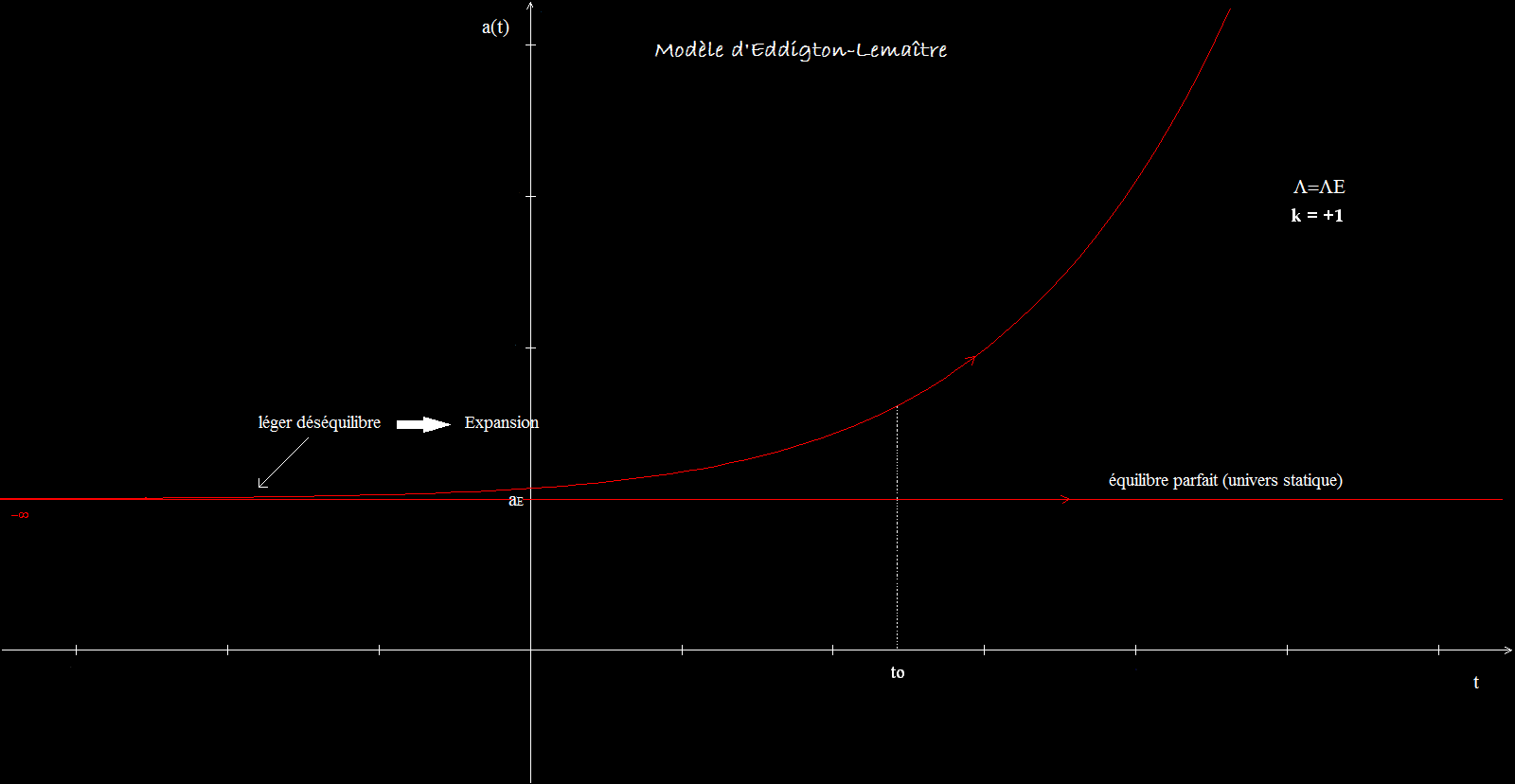
1er cas : L'univers d'Eddigton-Lemaître ( L =LE )
Persuadé que l'expansion de l'univers est une réalité (contrairement à Einstein à cette époque), Lemaître propose en 1927 un modèle d'univers sans big-bang mais en expansion. L'univers est là depuis toujours dans un état statique correspondant au modèle d'Einstein présenté en 1917, puis entre dans une phase d'expansion suite à une perturbation.
2ième cas : L'univers de Lemaître ( L > LE )
Dans ce modèle, Lemaître suggère que
l’univers possède un début dont l’origine serait la désintégration d’un
"atome-univers". L’univers connaîtrait alors une phase d’expansion rapide suite à
laquelle il entrerait dans une phase de stagnation plus ou moins longue
(suivant que L est plus ou moins proche de LE). Durant
cette seconde phase, il y aurait un équilibre presque parfait entre la gravité
et la répulsion provenant de la constante cosmologique. C’est lors de cette
phase que des fluctuations de densité apparaissent donnant naissance aux
étoiles puis galaxies et amas de galaxies. La formation de ces condensations de
matière perturberait l’équilibre et déclencherait alors une nouvelle phase d’expansion
que l’on observe aujourd’hui.
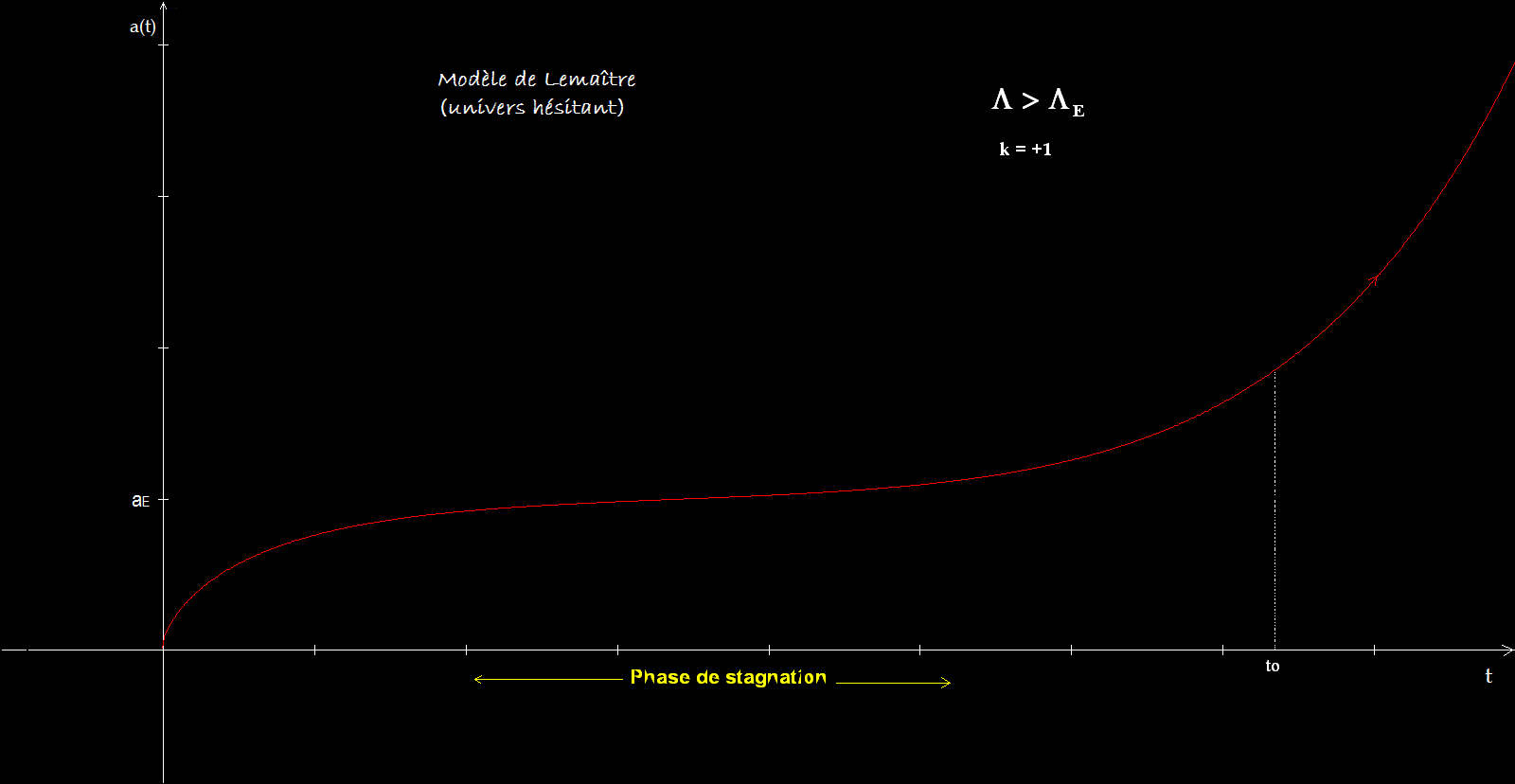
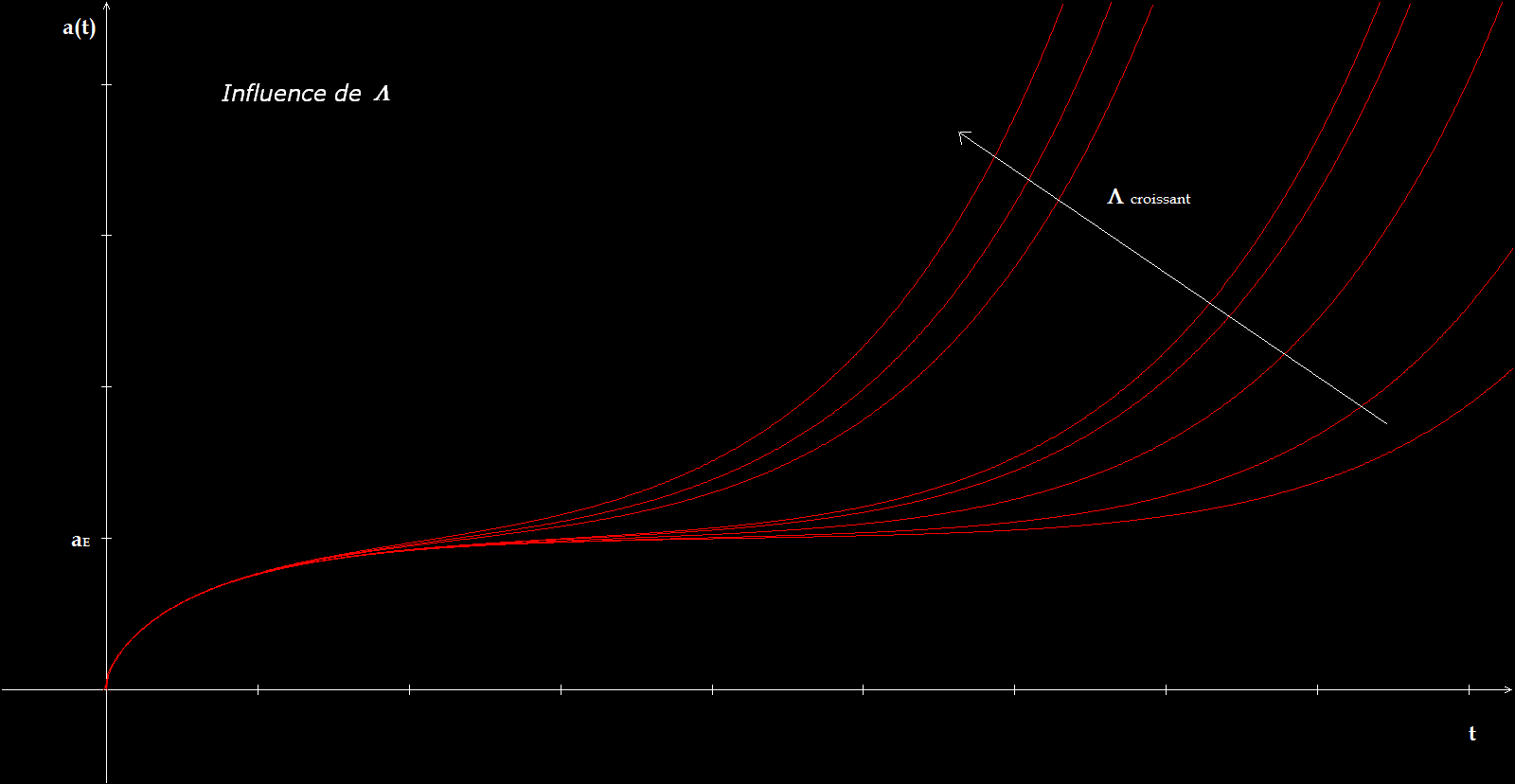
Plus la valeur de L s'écarte de LE et plus la phase de "stagnation" est courte.
3ième cas : L'univers à rebond ( L < LE )
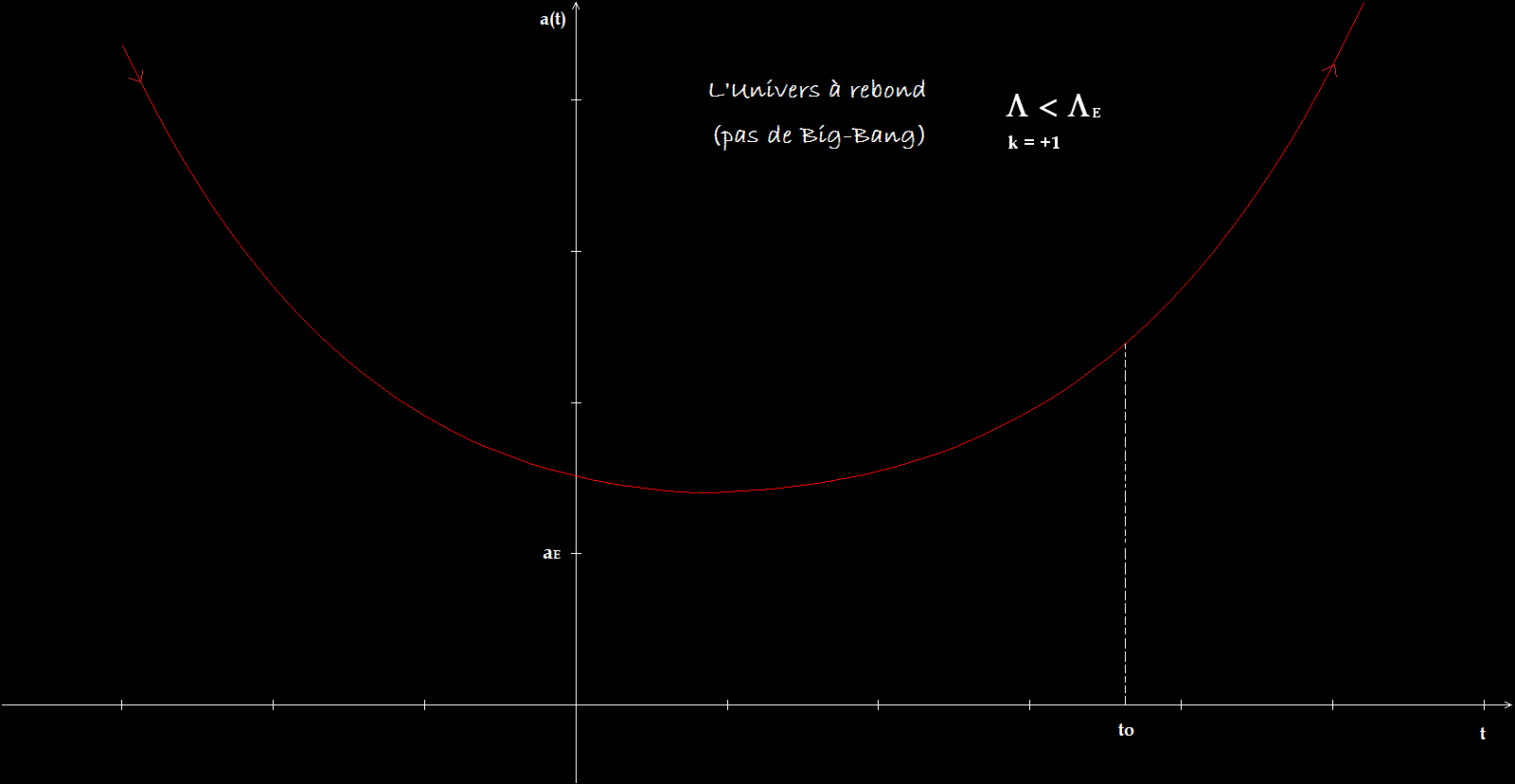
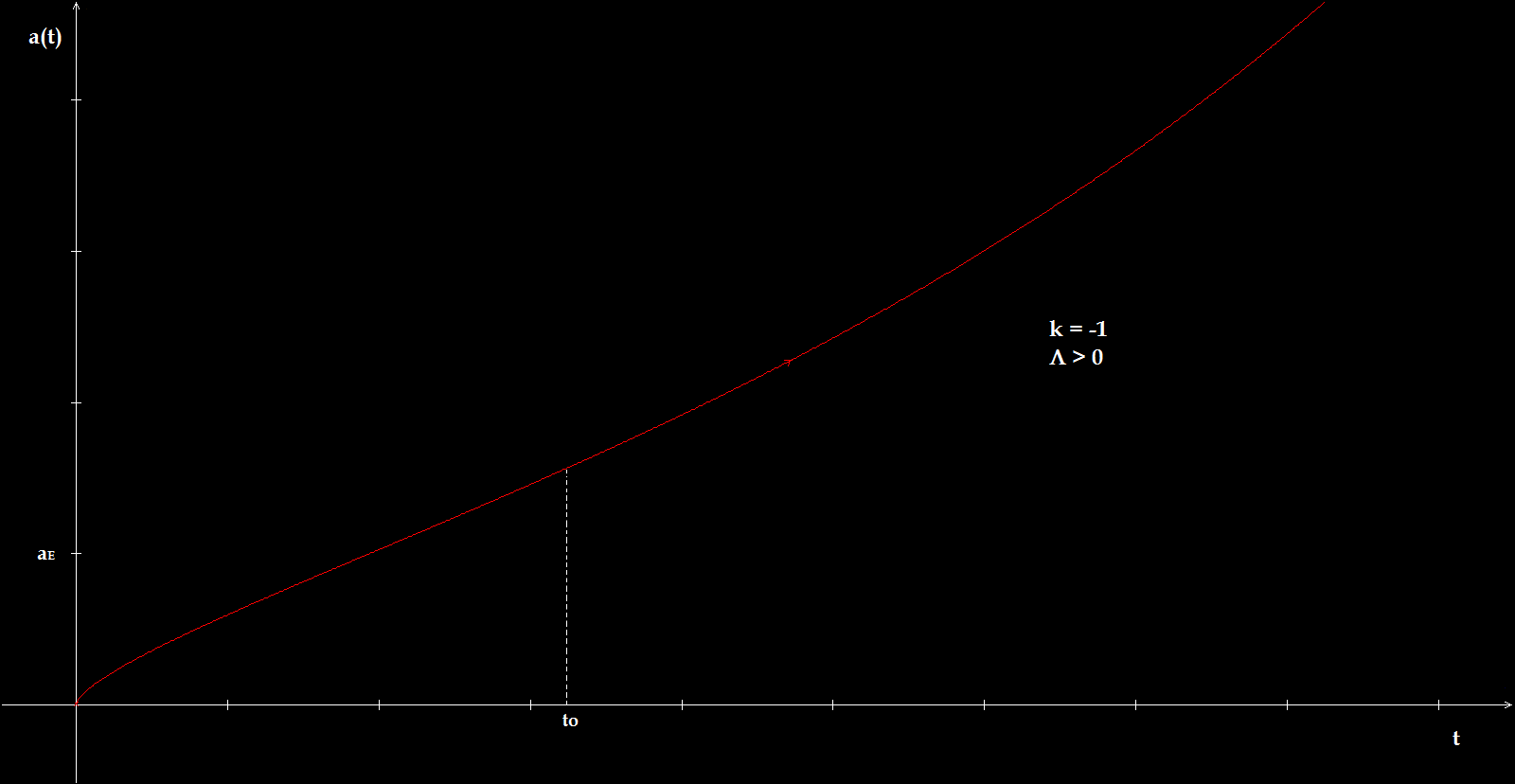
b-3) Univers de courbure négative (k= -1)
Dans le cas d'une courbure négative, tous les univers connaissent un Big Bang quelque soit la valeur de L.
5-5) Un modèle d'inflation: L'univers de De Sitter
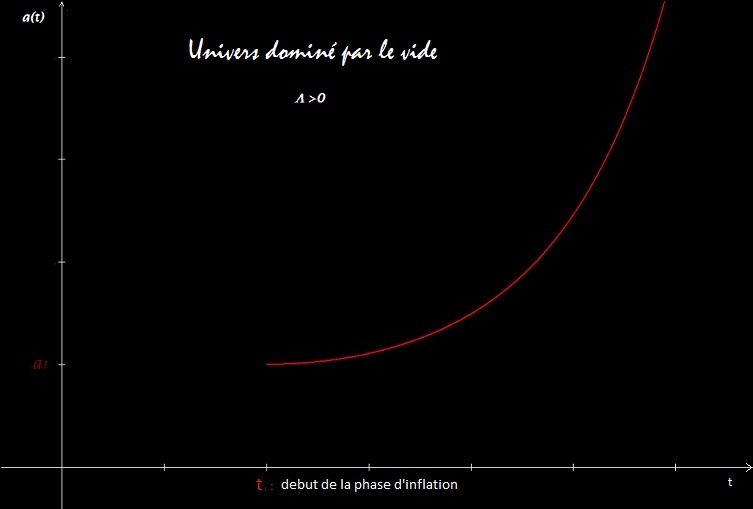
D'après le modèle standard, l'univers aurait connu une phase d'expansion extrêmement rapide au tout début de son existence. Ses dimensions auraient été multipliées d'un facteur 1025 en quelques 10-30s de quoi le rendre homogène et aplanir toute courbure initiale. Cette phase d'expansion serait dûe à un champ scalaire nommé "inflaton" et dont la densité d'énergie reste quasiment constante lors de la dilatation de l'univers. Dès lors, on peut modéliser l'inflation à l'aide de la constante cosmologique d'Einstein puisque la densité d'énergie qui lui est associée est elle aussi constante.
On considère pour cela un univers dominé par l'énergie du vide (jouée par la constante cosmologique L>0) et dont on peut négliger la densité d'énergie de matière:

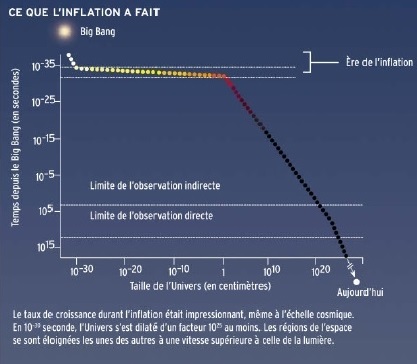
Source : dossier "Pour la science" n°83
5-6) Le modèle stationnaire (1948)
Dans
les années 1950, la plupart des physiciens avaient plus ou moins adopté la théorie du Big-Bang de
Georges Lemaître même si de nombreux problèmes subsistaient encore comme par exemple l’âge de l’univers.
D’après les mesures de Ho (environ 500 km.s-1.Mpc-1) l’univers
avait un âge maximum d’environ 2 milliards d’années alors que les géologues de
l’époque dataient déjà certaines roches
terrestres à environ 3,5 milliards d’années. La Terre serait plus âgée que
l’univers !
En
désaccord avec la théorie selon laquelle l’Univers serait né d’une « explosion »,
Fred Hoyle, Hermann Bondi et Thomas Gold , prônaient l’existence
d’un Univers stationnaire c'est-à-dire
un univers éternel (sans début) et immuable (même aspect). La théorie de l'état stationnaire offrait une alternative au problème
d'un commencement de l'Univers posé par le modèle standard. L'acte de création
unique était remplacé par un Univers qui se crée continuellement lui-même.
En effet l’expansion de l’univers
étant un fait avéré, de la matière devait être crée continument à partir du vide afin que l’univers resta
inchangé dans le temps comme l’affirmait les 3 physiciens (c’est le principe
cosmologique parfait imaginé par Hoyle : l’univers est homogène, isotrope
et identique à lui-même dans le temps) : les calculs de Hoyle conduisaient à un taux de création d'un atome
d'hydrogène par décimètre cube et par milliard d'années.
Le terme de « big-bang »
a été inventé par F.Hoyle lors d’une émission à la BBC en 1951 afin d'illustrer de façon un peu ridicule le modèle de Georges Gamow, fervent défenseur de la théorie de Lemaître. Georges
Gamow est d’ailleurs l’un des premiers à avoir prédit dans les années 40 que si
l’univers était passé par une phase dense et chaude, il devait exister
aujourd’hui un reliquat de cet état très chaud: le rayonnement fossile.
Néanmoins,
au début des années 60, lorsque les
quasars furent découverts en grand nombre, il fallut bien convenir que
la théorie de l'état stationnaire n'était plus crédible. Dennis W. Sciama
et Martin J. Rees remarquèrent qu'il existait beaucoup plus de quasars
dans le passé que de nos jours. Leur découverte démontrait une évolution
cosmologique, incompatible avec la théorie de l'état stationnaire. Le coup
d’arrêt final à la théorie de Hoyle, Bondi et Gold fut la découverte du fond
diffus cosmologique en 1965. L’origine, son spectre de corps noir et le fait que sa température était plus élevée par le passé ne
pouvaient pas être expliqués correctement par la théorie de l’univers
stationnaire.
6°) Grandeurs observables et données expérimentales
6-1) Quelques grandeurs utiles
a) La distance radiale comobile: Dcom
Soit un observateur situé à l'origine du référentiel comobile. Pour cet observateur, la distance radiale comobile Dcom d'un point dont les coordonnées sphériques sont (r,0,0) est obtenue en intégrant la partie spatiale de la métrique de FLRW réduite à sa composante radiale:
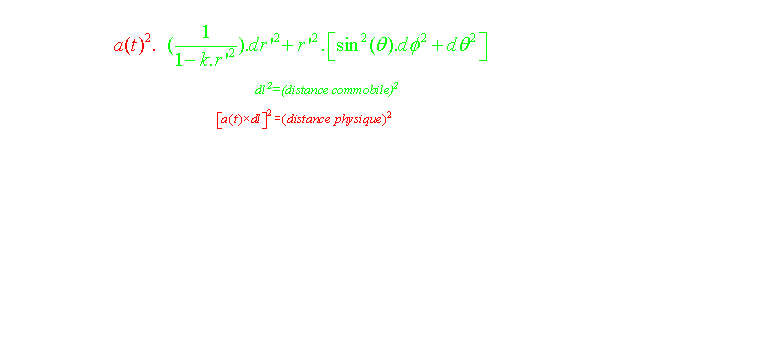
Bien que non mesurable, cette grandeur fixe de façon intrinsèque et indépendamment de l'expansion, la distance entre 2 points.
b) La distance physique radiale: Dp
Il s'agit de la distance géométrique entre 2 points de l'espace. Il s'agit d'une grandeur qui est fonction du temps et qui ne peut être mesurée qu'à un instant donné, ce qui n'est pas possible en pratique car toute mesure de distances ne peut se faire de façon instantannée. Il ne s'agit donc pas d'une grandeur directement accessible.
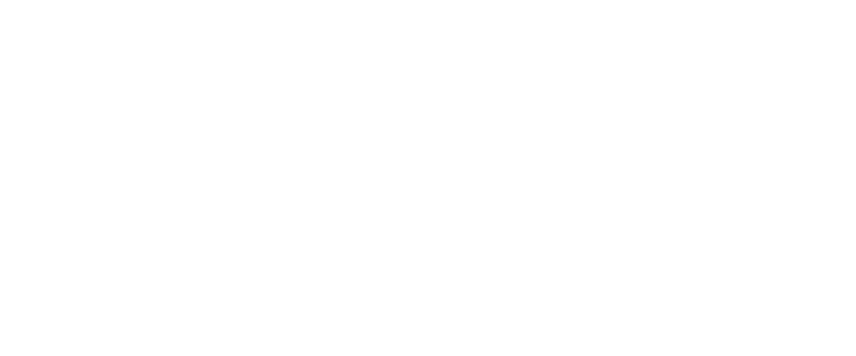
6-2) Grandeurs observables
a) Le décalage vers le rouge (redshift)
Le "redshift", ou décalage vers le rouge de la lumière, s'observe dans le spectre de tous les objets lointains. Il est dû à l'expansion de l'univers et à la vitesse relative entre les objets qui en résulte.
Si la distance radiale comobile entre nous et une galaxie donnée est constante au cours du temps, 2 photons successifs émis par cette galaxie devront parcourir des distances lumière différentes en raison de la dilatation de l'espace lui même. Le second photon aura une distance légèrement plus grande à parcourir et prendra donc du retard sur le premier ; Il sera reçu par l'observateur terrestre avec un léger décalage temporel plus grand que celui les séparant à leur émission.
Considérons 2 photons émis depuis une galaxie donnée aux instants te et te+ dte en direction d'un observateur O où ils arrivent aux instants to et to+dto. Comme il s'agit de lumière, on peut écrire pour chacun des photons que ds2 =0 e
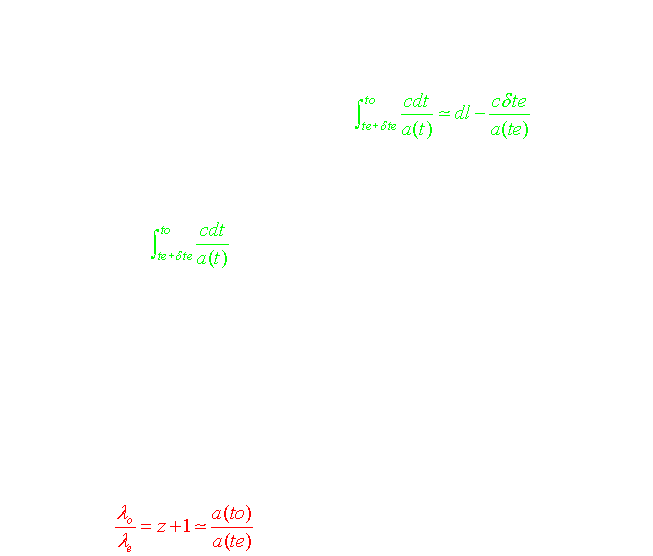 n
n 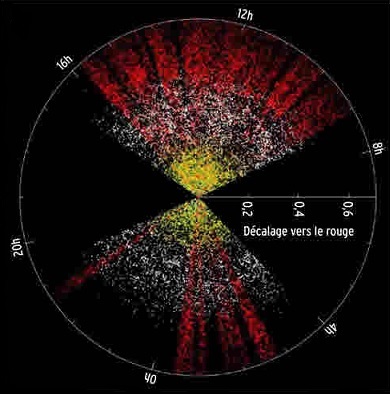
b) Le taux d'expansion: Ho
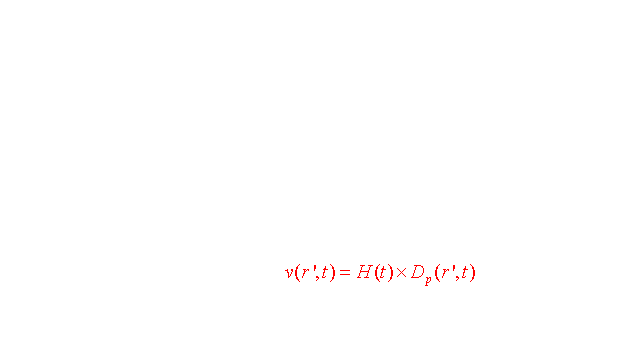
En réalité, il n'est pas possible d'obtenir directement la valeur de v(to) et Dp(to) pour en déduire celle de H(to) : les seules grandeurs accessibles aux mesures sont le redshift "z" et la distance-lumière (aussi appelée distance de luminosité)
Néanmoins, pour des distances relativement faibles (donc pour des redshifts petits), on peut obtenir la valeur de v(to) à partir de la mesure du redshift "z":

De même si les redshifts mesurés sont faibles, la valeur de Dp(to) est quasiment égale à Dl(to) que l'on obtient facilement à partir de la luminosité apparente d'une source lumineuse dont on connaît la luminosité intrinsèque (ex: les cépheides). C'est de cette façon que Hubble a obtenu sa loi de proportionnalité entre les vitesses de récession et les distances radiales et a ainsi pu en déduire la valeur de Ho.
c) La distance lumière: DL
La distance entre 2 points de l'espace peut aussi être définie par la distance parcourue par la lumière pour les joindre. Cette distance est équivalente au temps de voyage mis par la lumière pour joindre les 2 points de l'espace séparée d'une distance comobile r'. Dans un univers en expansion, La distance-lumière ne coincide pas avec la distance physique Dp entre les objets puisque celle-ci varie continûment pendant le voyage de la lumière.
Si "dl" est la distance comobile infinitésimale séparant 2 points de l'espace, la distance-lumière DL, qui dépend de l'instant d'émission te, satisfait la relation ci-dessous:
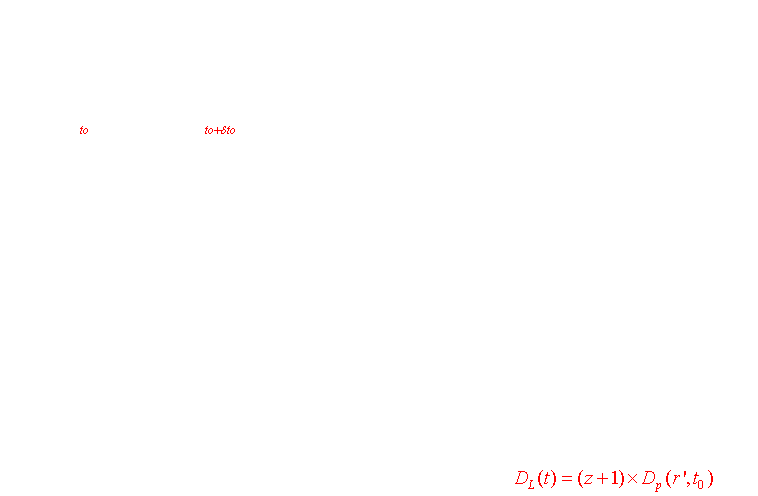
Autre façon:

En pratique, la distance luminosité s'obtient en mesurant la luminosité apparente d'une source lumineuse dont on connaît la luminosité intrinsèque (ex: Céphéides, SNIa): 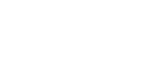
d) La distance angulaire : DA
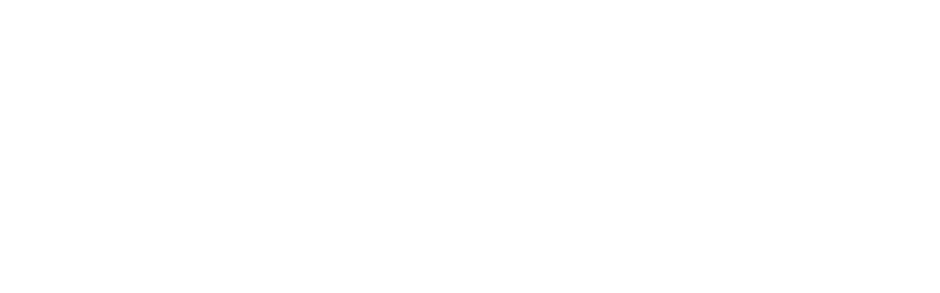
6-3) Résultats expérimentaux et paramètres cosmologiques
a) Relation "redshift"-"distance-lumière" et détermination des valeurs de Ho et qo : les 2 expériences "Supernovae Cosmology project" et "High-Z Supernovae Surch Team"

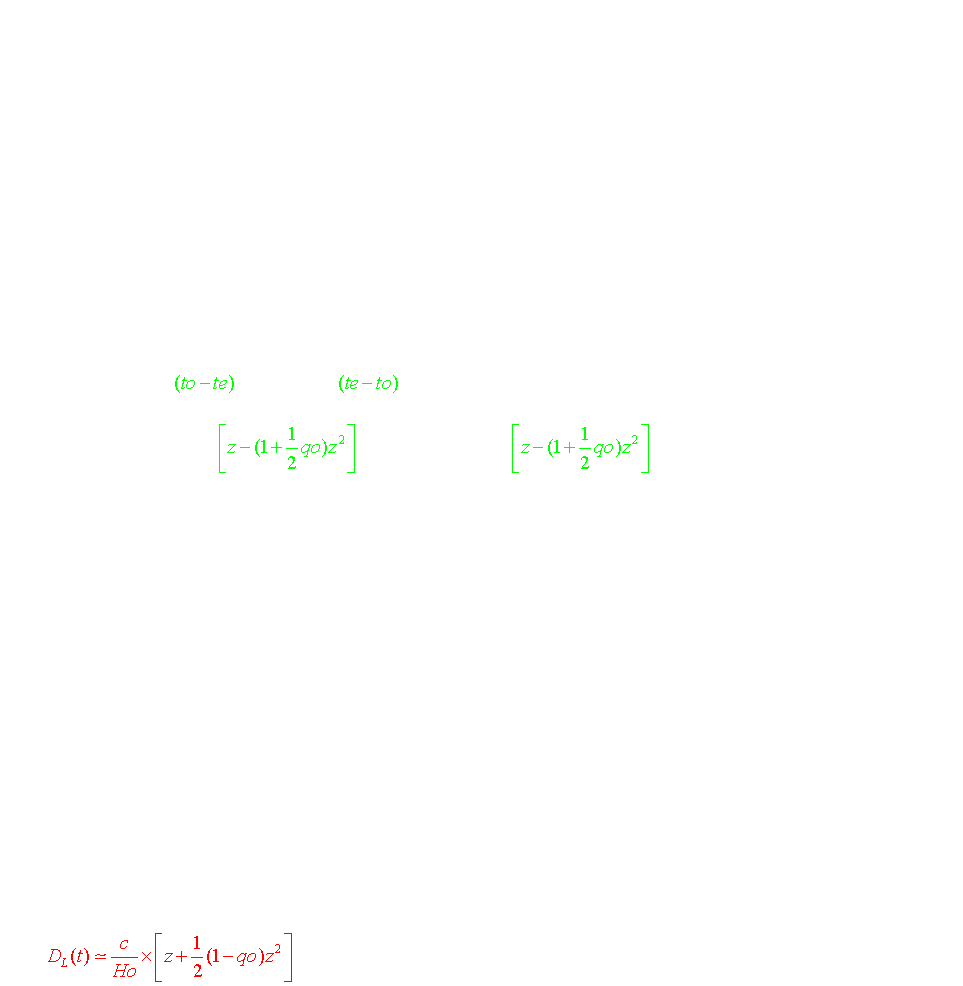
Remarque: pour des redshifts très petits, le terme en z2 est négligeable et on retrouve dès lors la relation établie par E. Hubble : 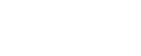
En pratique, il suffit de mesurer le redshift d'objets lumineux ainsi que la distance à laquelle ils se trouvent de la Terre pour en déduire les valeurs de Ho et qo
L'observation d'un grand nombre de supernovae de type SNIa ("Supernovae Cosmology project" et "High-Z Supernovae Surch Team") a permis de tracer la courbe DL= f(z) et d'en déduire une valeur relativement précise de Ho et qo:
|
|
D'après les dernières mesures publiées en 1998, on trouve Ho = 72 km/s/Mpc et qo = -0,6 ce qui signifie que l'expansion de l'univers s'accélère. Ces résultats sont en assez bon accord avec ceux obtenus grâce à la mission Planck même si une différence persiste...c'est ce qu'on appelle la "tension de Hubble". Pöur ma part, les résultats de Planck sont plus réalistes que ceux donnés avec les chandelles standards que sont les SNIa. Sont-elles aussi standards que ça ?
|


b) Analyse du fond diffus cosmologique et paramètres cosmologiques
b-1) L'isotropie miraculeuse du FDC et le phénomène d'inflation cosmologique
b-1-1) Une idée novatrice
Selon le scénario de l’inflation, l’univers a connu à son
tout début une phase d’expansion fulgurante
au cours de laquelle les distances ont été multipliées d’un facteur 1025
en une fraction de seconde (de l’ordre de 10-30 s). Cette phase
d’inflation a été imaginée par plusieurs physiciens tels A.Guth en 1983
et A.Linde la même année, afin de résoudre plusieurs difficultés liées au
modèle cosmologique classique communément
admis jusqu’alors. On peut citer :
- Le problème de la platitude de l’univers : Pour que
l’univers soit de courbure quasiment nulle aujourd’hui (ce qui est vérifié par plusieurs
expériences différentes et notamment par la mission européenne
« Planck ») il aurait fallu que ça soit exactement le cas dès le début: au temps de Planck (10-43
s), la courbure de l'univers aurait du être nulle à 10-60
près.... A moins d’une coïncidence extraordinaire, il n’y a aucune raison pour que ce fusse le cas.
Avec le phénomène
d’inflation, peut importe la courbure initiale de l’univers, l’expansion vertigineuse a simplement
aplani toute courbure initiale de
l’espace.
- Le problème de
l’horizon : le fond diffus cosmologique à 2,7 °K est globalement isotrope
alors qu’il n’y a aucune raison pour que 2 parties du FDC non causalement
reliées (c'est-à-dire qui n’ont pas pu être reliées par un phénomène physique)
soient à la même température.
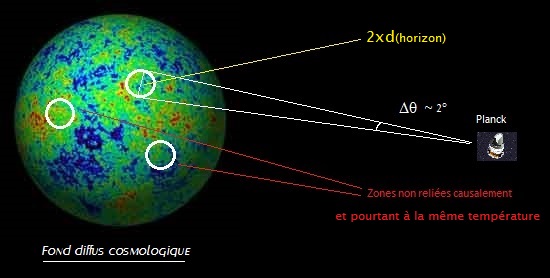
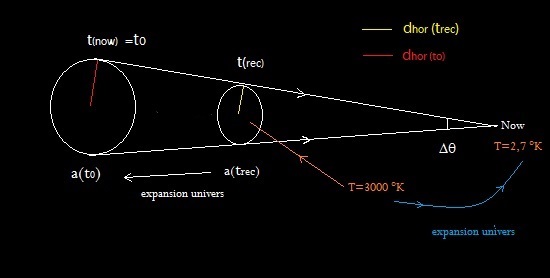
(Un calcul un peu plus réaliste faisant intervenir la densité de matière et l'énergie sombre donne un résultat du même ordre de grandeur à savoir entre 2° et 4°)
L’inflation assure que ces régions étaient en réalité en contact, car initialement suffisamment
proches pour que les conditions physiques régnant dans ces régions aient eu le temps de
s’équilibrer. Le phénomène d’inflation n’a fait que dilater de façon titanesque
cette zone déjà homogène.
- L’hétérogénéité de l’univers à
« petite » échelle. Il a du
exister de petites inhomogénéités primordiales responsables des structures
(galaxies, amas, filaments ..) que nous observons aujourd’hui. Ces
inhomogénéités primordiales sont visibles aujourd’hui dans le fond diffus
cosmologique où l’on observe de petites anisotropies (de l’ordre de 10-5
°K) au niveau de la température. L’origine de ces inhomogénéités primordiales
est difficile à expliquer dans les modèles cosmologiques classiques.
Avec l’inflation,
les anisotropies du FDC auraient simplement pour origine les fluctuations
quantiques inévitables du champ scalaire qu’est « l’inflaton ».

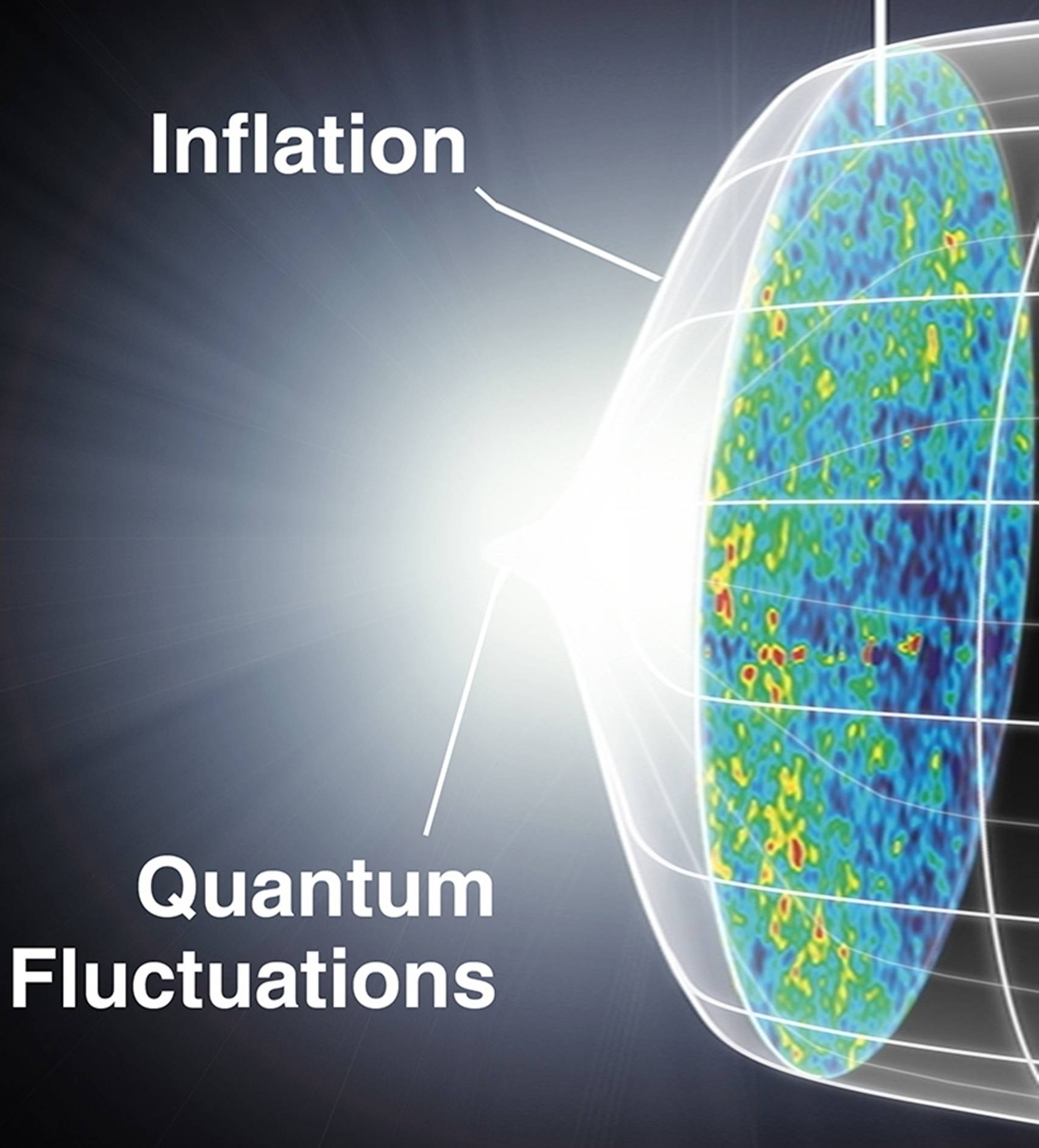
b-1-2) Le modèle théorique
Le
scénario inflationniste original de A.Guth supposait que l’univers était
initialement piégé dans un faux vide duquel il aurait échappé par effet tunnel
quantique. Malheureusement, le processus d’effet tunnel (équivalent à une transition de phase du
premier ordre) engendre de trop grandes inhomogénéités comparées à celles observées
de nos jours notamment dans le fond diffus cosmologique. Les nouveaux modèles inflationnaires utilisent désormais des
champs scalaires capables de reproduire une phase d’expansion très rapide. Ces
champs scalaires s’appuient sur les modèles de théories des champs de la
physique des particules qui prédisent l’existence de champs scalaires lors des
brisures spontanées de symétrie telle que ce fut le cas lors de la séparation
de l’interaction forte et électrofaible ou bien encore lors de la séparation de l'interaction faible et électromagnétique. Ce type de champs aussi appelés champs de "quintessence", sont considérés comme de simples champs de matières non couplés directement avec la gravité: leur influence sur la structure et la dynamique de l'espace-temps n'intervient que par l'intermédiaire de leur tenseur "énergie-impulsion".
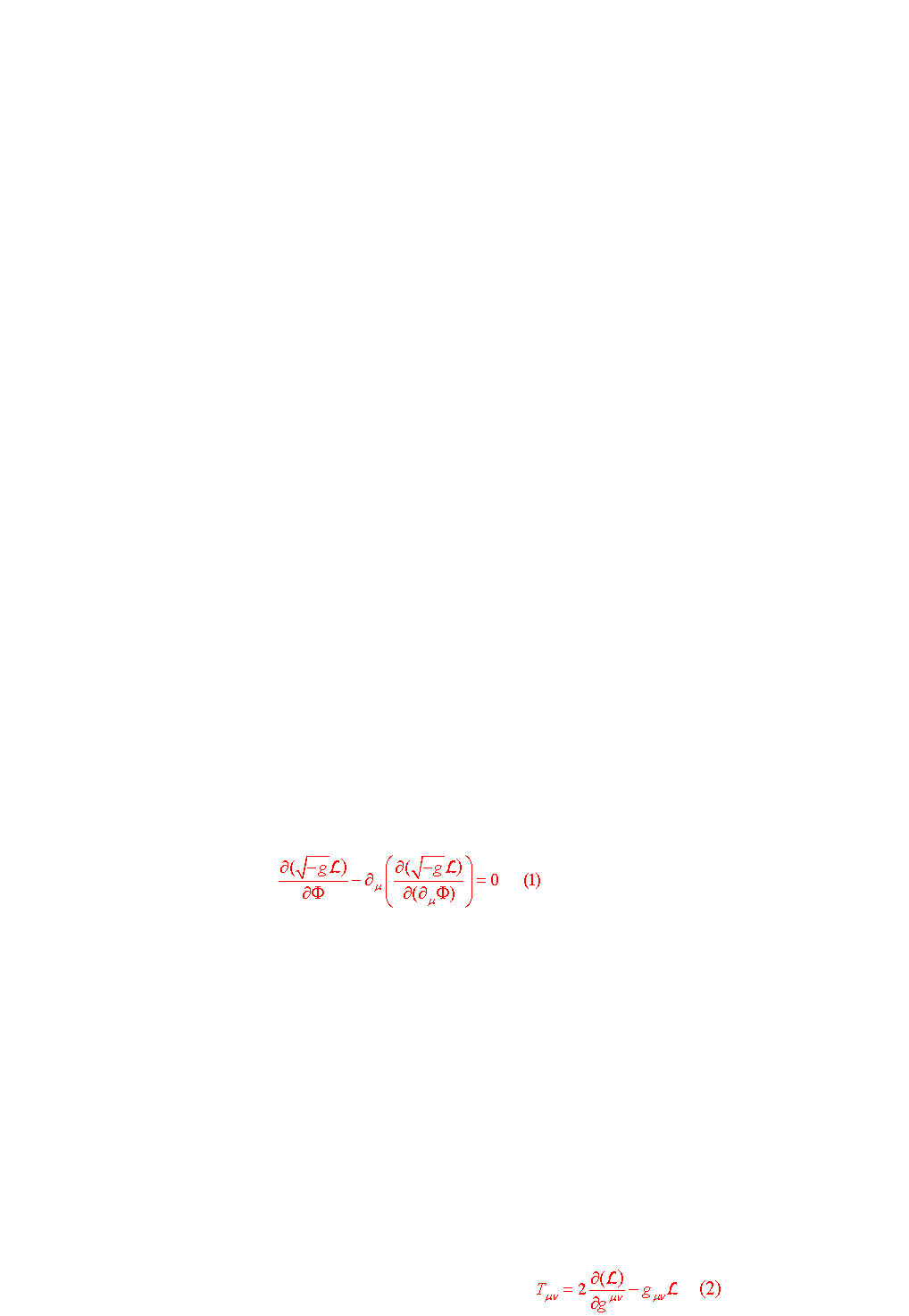
 *
*
Equations du champ couplé au tenseur "énergie-impulsion" du champ scalaire
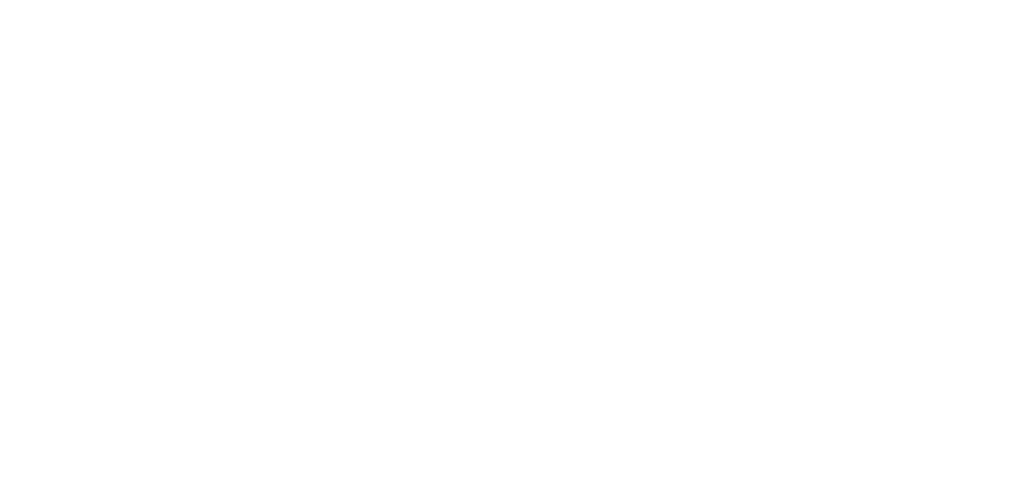
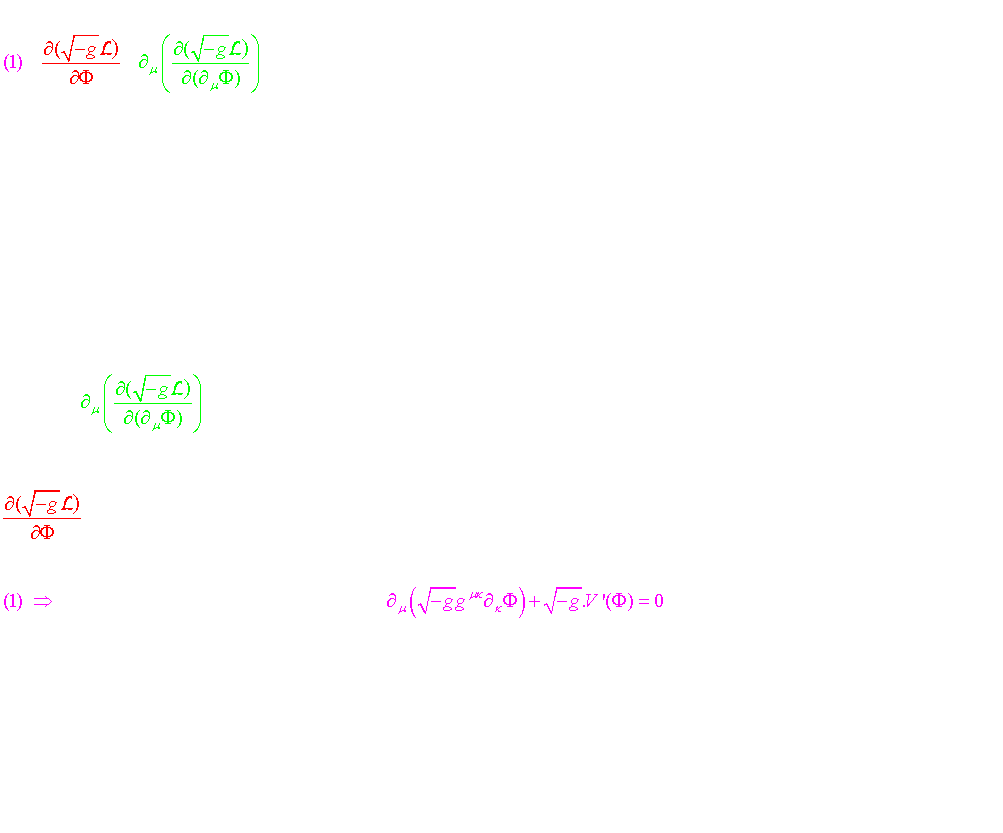

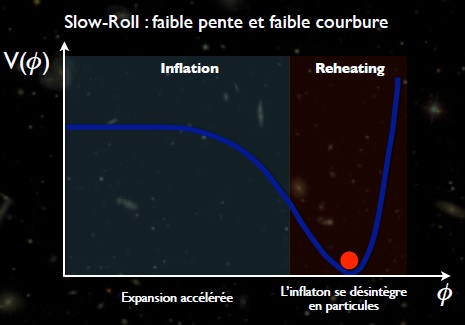
b-1-2-a) Conditions nécessaires pour obtenir une phase d'inflation: " The slow roll condition"

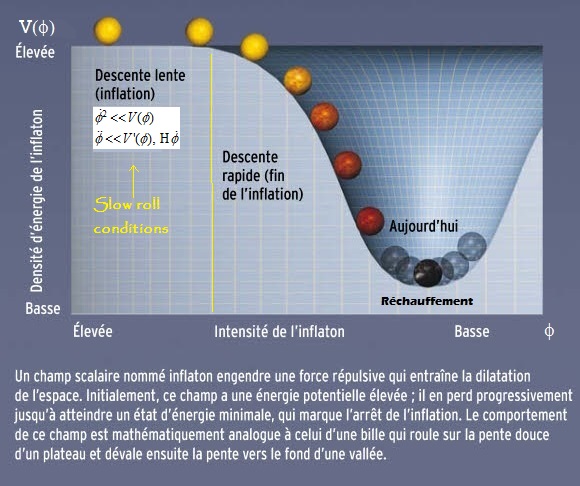
Un champ scalaire permettant une phase d'inflation doit donc obéir dans un premier temps à la condition : ![]()
La phase d'inflation doit aussi durer relativement "longtemps" :
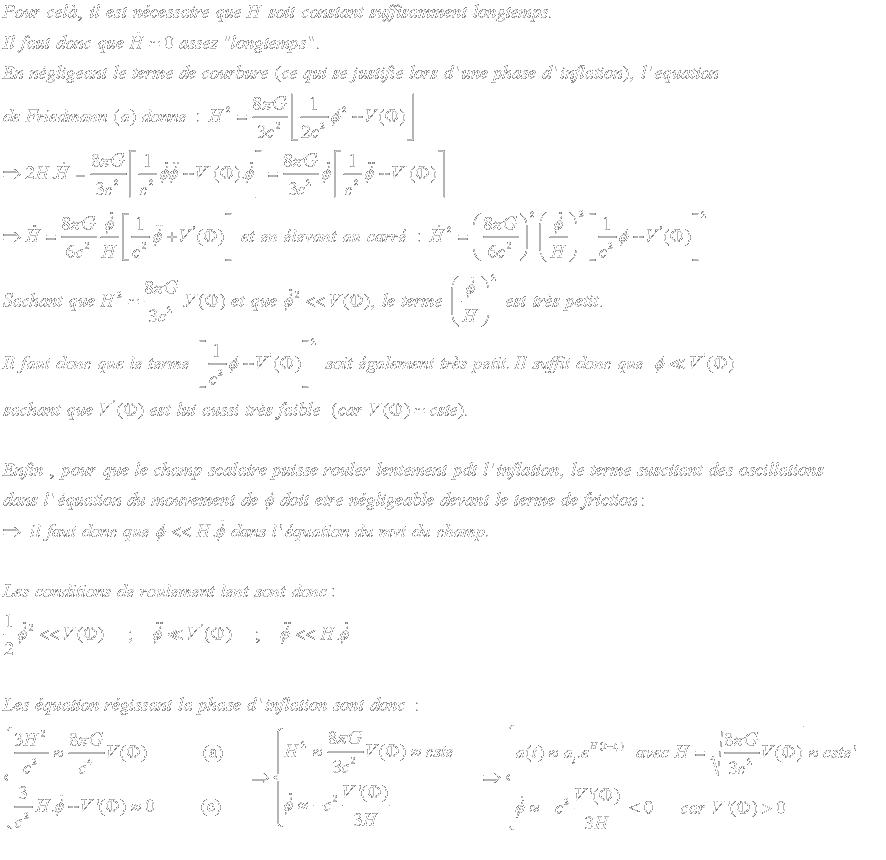
Une dernière contrainte sur le potentiel est lié au nombre de "e-folds" :r
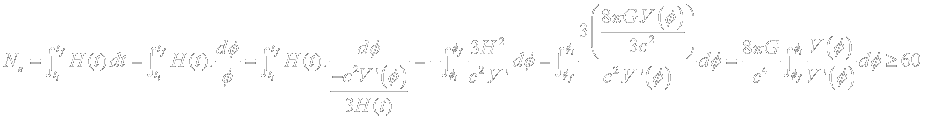
b-1-2-b) Fin de l'inflation et phase de réchauffement
A la fin de l’inflation, presque
toute la densité d’énergie de l’Univers est contenue dans le champ scalaire nommé "l’inflaton". Ce champ doit,
d’une manière ou d’une autre, se désintégrer et transmettre son énergie à
On envisage pour cela différents potentiels d'inflation, chacun représentant des modèles d'inflation légèrements différents (inflation à un champ, inflation hybride avec champ lourd, inflation multichamps légers, etc..) mais tous obéissant aux conditions de "slow roll". Parmi tout ces modèles, le modèle à champ large aussi appelé "inflation chaotique" est le modèle adopté aujourd'hui par la majorité des cosmologistes. Il décrit de façon relativement simple la manière dont s'effectue la fin de l'inflation; Dans ce modèle, la valeur initiale du champ scalaire prend une valeur arbitraire, c'est à dire de façon chaotique. Dans certaines régions de l'univers, le champ se situe assez loin du minimum de son potentiel. Si le potentiel est assez plat, le champ va rouler lentement et suffisamment longtemps pour que cette région de l'espace subisse une inflation fulgurante avant que le champ finisse enfin par s'immobilser au fond du minimum de potentiel, signant ainsi la fin de l'inflation. Pour d'autres régions de l'univers, le champ est déjà proche du fond de la cuvette d'énergie potentiel et aucune inflation n'a lieu. L'univers peut ainsi être inhomogène aux très grandes échelles alors que notre univers observable serait quant à lui issu d'une région ayant subi une inflation qui l'aurait ainsi "lissé" pour le rendre globalement homogène et isotrope. En raison des fluctuations quantiques, certaines régions de l'univers où le champ initial était déjà proche de la cuvette, peuvent à leur tour entrer dans une phase d'inflation si le champ scalaire remonte subitement dans le potentiel suite à une fluctuation quantique: on parle alors d'inflation éternelle puisque chaque partie de l'univers peut être assujetti à ce processus. On aboutit ainsi à un univers-bulles où chaque bulle représente une région subissant, ou ayant subie une inflation: on parle alors de multivers ou chaque univers bulle peut être régi par des lois physiques différentes.
UNIVERS BULLES
Forme du potentiel lors de la phase de réchauffement:

Cette équation est la même que pour une balle roulant sur le potentiel avec un terme de friction. Un tel mouvement présente 2 régimes différents: un premier où la friction domine et la balle descend lentement le potentiel et un deuxième où celle-ci fait de rapides oscillations autour du minimum pour finir par s'y stabiliser. C'est lors de ses oscillations amorties que l'énergie restante de l'inflaton sert à engendrer matière et rayonnement via des couplages appropriés avec les différents champs de matière. S'en suit enfin une période de thermalisation des particules ainsi produites: L'univers est dès lors en équilibre thermique comme le prouve le FDC. Néanmoins aucune théorie ne permet de passer simplement d'un potentiel de type "slow roll" à un potentiel caractéristique de la phase de réchauffement.
b-2) Anistropies primordiales dans le FDC et oscillations baryoniques acoustiques (BAO)
b-2-1) Les oscillations baryoniques acoustiques (généralités)
L'existence de structures telles que les étoiles, les galaxies, ou les amas de galaxies suggère la présence de petites fluctuations au début de l'histoire de l'Univers, fluctuations à l'origine des anisotropies du fond diffus cosmologique. Ces fluctuations trouvent leur origine dans les fluctuations quantiques du champ scalaire responsable du phénomène d'inflation cosmique (l'inflaton). Ces fluctuations primordiales ont ensuite été projetées via l'inflation à des échelles cosmologiques où elles ont ensuite évolué sous l'ère de la domination radiative puis de la matière.
En raison de ces fluctuations primordiales, des zones de surdensités vont apparaître dans le plasma originel formé juste après la nucléosynthèse c'est à dire quelques minutes après le big-bang. Ce plasma est principalement constitué de matière noire, de neutrinos mais aussi de photons, d'électrons et de baryons (essentiellement protons et noyaux d'hélium). Une fois l'égalité matière-rayonnement dépassée (t ~100 000 ans) l'expansion est surtout gouvernée par la matière et les zones de surdensités de matière vont s'effondrer sous l'action de la gravité. La température dans les zones surdenses augmente, conduisant alors à l'augmentation de la pression de radiation. A cette époque, les baryons sont fortement couplés aux photons via les électrons (par diffusion compton puis thomson), et la forte pression de radiation va dès lors contribuer à diminuer l'amplitude des zones de surdensités dans lesquelles les baryons avaient plongé, entrainant à son tour une diminution de la pression de radiation. La gravité l'emporte à nouveau et entraine un nouvel effondrement et ainsi de suite. Photons et baryons connaissent donc une phase d'oscillation de densité appelée "oscillations baryoniques acoustiques". Il apparait ainsi des ondes de surdensité se propageant dans le plasma baryons-électrons-photons et dont la vitesse de propagation est notée "Cs".
En considérant que les perturbations scalaires sont adiabatiques, un calcul simplifié permet d'obtenir une valeur approchée de Cs.
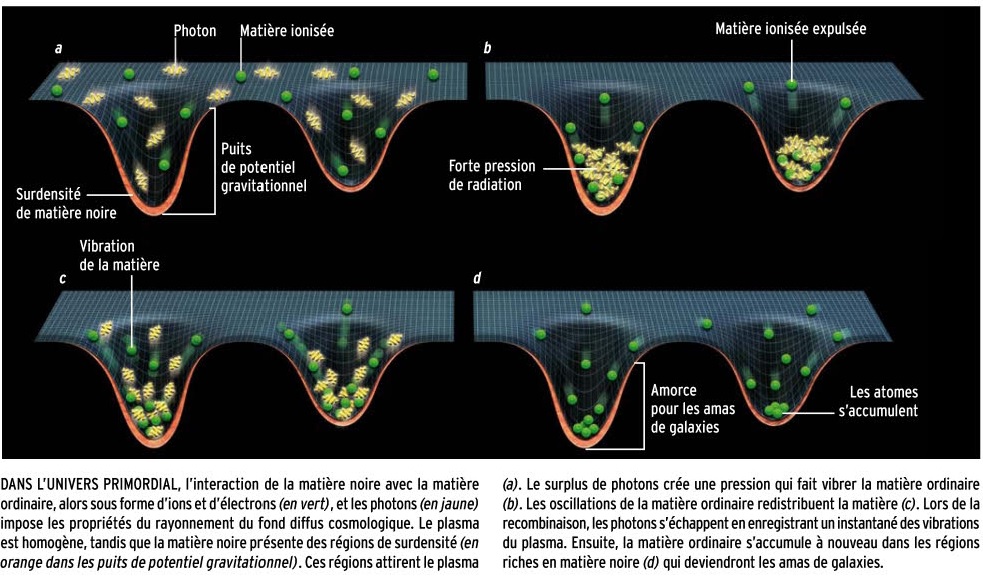
Environ 380 000 ans après le big-bang, la température devient suffisamment basse pour que les électrons et les protons s'assemblent et forment des atomes d'hydrogène mais aussi d'hélium ; C'est le "découplage matière-lumière". A ce moment, les électrons interagissent beaucoup moins avec les photons et la pression radiative n'est plus suffisante pour que l'onde acoustique puisse continuer sa propagation. Les zones de surdensités produites par l'onde se figent comme si on gelait subitement l'eau d'un lac après y avoir jeté une pierre. Il se forme alors une coquille d'environ 150 Mpc comobiles de rayon autour des surdensités originelles. Le puit de potentiel gravitationnel engendrée par la matière noire rappelle la majeur partie des baryons au centre de la coquille alors qu'une partie de la matière noire tombe dans le puit de potentiel gravitationnel crée par la surdensité de baryons située à rs =150 Mpc.

L'horizon acoustique (rayon comobile de la coquille sphérique= distance comobile parcourue par l'onde sonore)

Si on tient compte du fait que la vitesse du son varie avec la densité de rayonnement au cours du temps c'est à dire en fonction du redshift "z"
Alors on peut appliquer la relation établie par Eisenstein et Hu, à savoir pour un modèle sans courbure:
Rque : Ce dernier résultat dépend des différents paramètres cosmologiques utilisés (notamment les valeurs de Wk , Wbaryon ,Wm et h) si bien qu'une détermination expérimentale de la valeur de rs donnera des indications sur le choix du modèle théorique le mieux adapté pour décrire fidèlement l'univers observable.
Ces zones de surdensité de matière ( r = 0 et r = rs) vont devenir les lieux privilégiés de formation des futurs galaxies et de leur accumulation sous forme d'amas. Ainsi, si on considère un grand nombre de galaxies et que l'on mesure la distance entre 2 paires, il devrait apparaître un excès de ces paires pour une valeur de distance proportionnelle à rs au facteur d'échelle a(t) près, comme on le verra plus tard.
b-2-2) Anisotropies du FDC
Les différentes zones de surdensité de matière issues des BAO vont laisser leur empreinte sur la température des photons au moment du découplage et donc sur le rayonnement fossile que l'on capte aujourd'hui. Certaines zones du FDC doivent donc présenter des excès et défauts de température par rapport à la moyenne qui vaut T=2,728 °K. Ces fluctuations de températures sont de l'ordre de 10-5 °K mais bien visibles sur la carte en température extraite des mesures du satellite "Planck" comme on peut le voir ci-dessous:
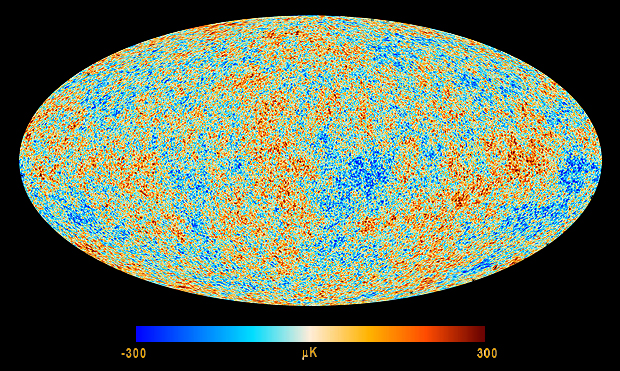
Trois types de fluctuations du plasma baryons-photons sont nécessaires pour décrire les anisotropies primaires de température du FDC:
- Les fluctuations de densité du plasma : les zones plus denses sont plus chaudes si bien qu'au moment du découplage, les photons qui s'échappent auront une énergie et donc une température plus élevée que la moyenne alors que les photons issus d'une zone de sous-densité auront une température légèrement plus faible.
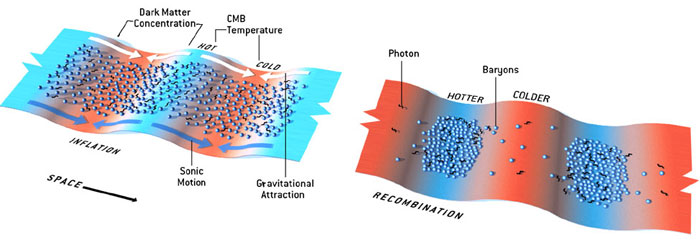

- Les fluctuations liées au champ gravitationnel : Les photons présents dans une zone de sur-densité au moment du découplage vont perdre de l'énergie pour s'échapper du puit de potentiel gravitationnel; Ils subiront un décalage vers le rouge et seront donc plus froid que la moyenne. Inversement les photons provenant d'une zone de sous-densité sortiront avec une température légèrement plus élevée. Cet effet est dénommé effet "Sachs-Wolfe" . Aux échelles plus grandes que l'horizon sonore ( Q >1° ) les anisotropies dépendent uniquement du spectre initial des fluctuations du potentiel engendrées elles-même par les fluctuations quantiques primordiales. Sur le spectre de puissance angulaire du FDC, cette partie s'appelle "le plateau de Sachs-Wolfe". L'analyse de cette partie du spectre permet de déterminer la valeur du potentiel gravitationnel à la fin de l'inflation et donc certaines caractéristiques concernant ce phénomène. L'effet Sachs-Wolfe sur la température vaut:

-Les fluctuations du champs de vitesse: En raison de l'effet Doppler, la vitesse du plasma le long de la ligne de visée augmente ou diminue la température des photons qui s'échappent. Si la sur-densité se dirige vers nous, les photons verront leur longueur d'onde décalée vers le bleu donc plus chaud, alors que si la zone de sur-densité s'éloigne de nous les photons paraîtront légèrement plus froid, leur longueur d'onde étant décalée vers le rouge. Cet effet se traduit sur la température par:
La contribution de chacun de ces effets en fonction de l'échelle angulaire doit être prise en compte pour décrire les anisotropies primaires de température du FDC au moment du découplage. On pourra trouver une large documentation (articles, thèses etc..) décrivant dans le détail ces différents processus physiques.
A ces fluctuations primaires, doivent également être prises en compte toutes les fluctuations liées aux différents phénomènes physiques que vont subir les photons lors de leur long trajet les menant ici sur Terre aujourd'hui; Ceux sont les fluctuations secondaires et dont il faut tenir compte pour analyser correctement les données fournies par le satellite Planck. Parmi les principales fluctuations secondaires, on peut distinguer:
- L'effet Rees-Sciama dû aux variations temporelles des potentiels gravitationnels engendrées par l'effondrement des différentes structures après le découplage. Lorsqu'un photon du CMB traverse un puit de potentiel gravitationnel variable au cours du temps, le gain d'énergie emmagasiné par le photon lorsqu'il tombe dans le puit et la perte d'energie qu'il subit pour s'en extraire ne se compensent pas, ce qui entraine une modification de la longueur d'onde du photon ayant traversé cette zone. Les variations de température sur le FDC sont de l'ordre de 10-6 °K
- L'effet Sachs-Wolfe intégré (ISW) qui tient compte des variations temporelles des potentiels gravitationnels que vont progressivement traverser les photons lors de leur long trajet, entrainant également une modification de la longueur d'onde des différents photons du CMB. Cet effet est surtout notable à grande échelle en présence d'énergie noire car les photons du FDC gagnent de l'énergie au moment de remonter pour sortir du puit gravitationnel car ce dernier a été étiré par l'expansion de la toile spatio-temporelle et est devenu moins profond.
- L'effet Sunyaev-Zel'dovich thermique provenant de l'interaction des photons du CMB avec les électrons chauds des amas de galaxies qu'ils vont rencontrer et modifiant ainsi leur énergie par diffusion compton inverse. Une partie de l'énergie des électrons chauds est transférée aux photons du CMB qui voient leur longueur d'onde légèrement diminuer.
Si l'amas est animé d'une vitesse par rapport au FDC, l'effet doppler induit un second effet appelé "effet Sunyaev-Zel'dovich cinétique".
- L'effet de lentilles gravitationnelles engendrées par les amas et modifiant la trajectoire des photons. Cette effet est assez faible sur le spectre en température du FDC mais peut être important pour la polarisation.
- La réionisation de l'univers par la lumière des premières étoiles (entre 800 millions d'années et un millard d'années) provoquant de nouvelles diffusions Compton avec les électrons libérés et dont l'effet est de réduire l'amplitude des anisotropies.
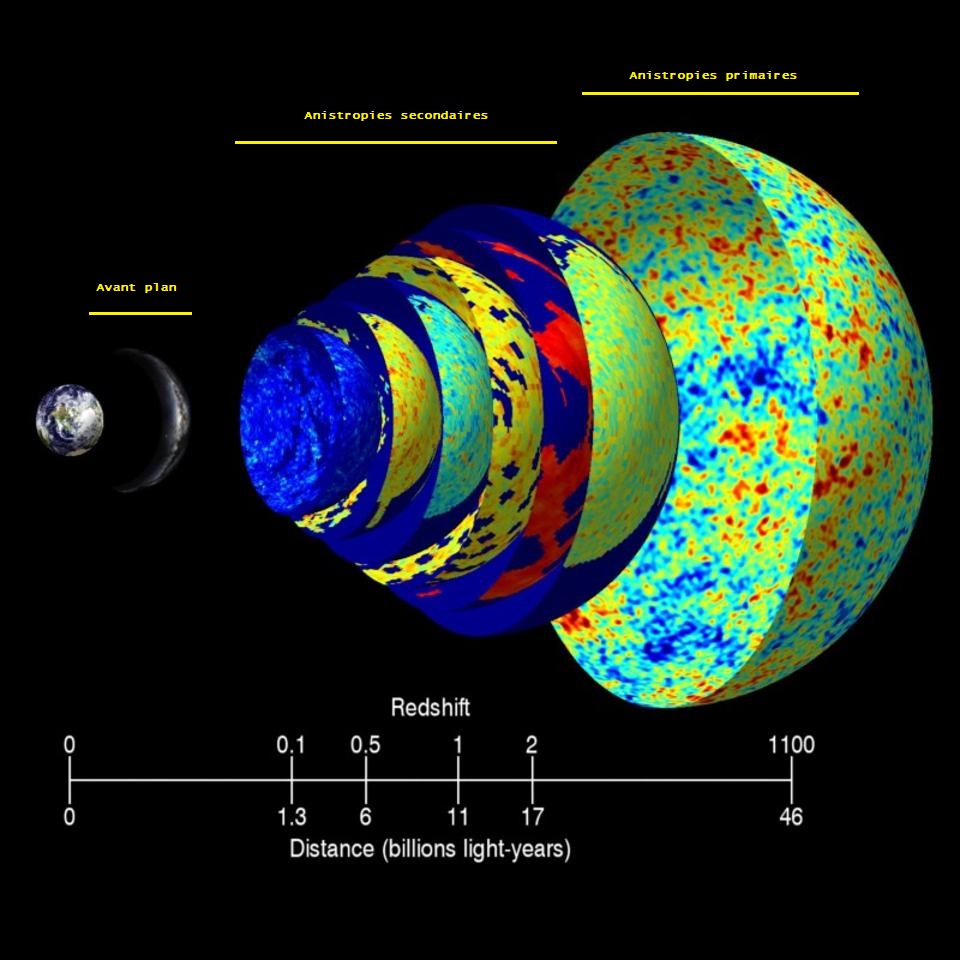
Enfin il faut également tenir compte de toutes les perturbations liées à notre galaxie c'est à dire les émissions de premiers plan:
- L'effet doppler lié au mouvement de la Terre par rapport au référentiel du FDC et qui se traduit par une anistropie dipolaire. Ce mouvement est la somme des mouvements de rotations de la Terre autour du Soleil, du Soleil autour du centre de la galaxie et du déplacement de la galaxie au sein de l'amas local. La variation de température dû à cet effet doppler sur le FDC est d'environ +/- 3,36 mK.
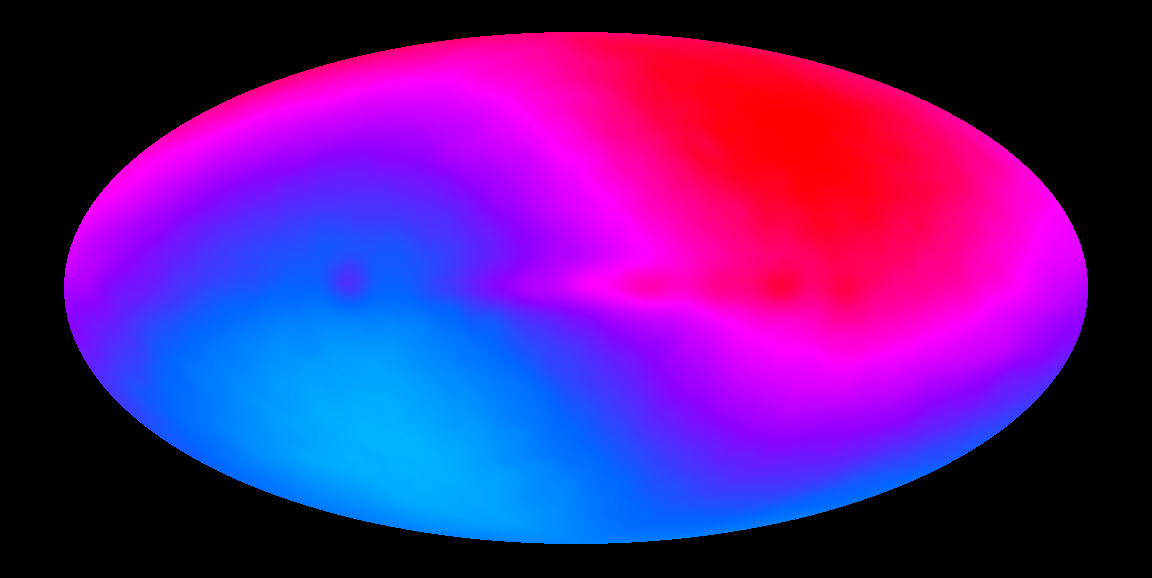
- L'émission thermique de la poussière interstellaire.
- L'émission synchrotron des électrons ultra-relativistes dans le champ magnétique ambiant.
- Le rayonnement de freinage des électrons dû à la présence d'ions dans le milieu, appelé émission Bremsstrahlung ou encore émission "free-free".
b-2-3) Le spectre de puissance du FDC
De façon simplifiée , il s'agit d'analyser les différentes corrélations au niveau de la température qui peuvent exister entre 2 points de la carte du FDC en fonction de l'échelle angulaire.
Le signal étant réparti sur une surface sphérique, les fluctuations de température sont décomposées en harmoniques sphériques:

Toute l'information relative aux fluctuations de température est contenue dans les valeurs des "alm" ,amplitude associée à chaque harmonique Ylm, mais la moyenne sur la sphère des fluctuations de température étant nulle, on aura <alm>=0
On s'interrèse dès lors à la variance ![]() qui peut être reliée à la fonction de corrélation à 2 points des fluctuations de température sur la carte et qui est notée "Cl". Cette fonction représente l'excès de probabilité de trouver 2 surdensités thermiques
à une certaine distance par rapport à une distribution thermique uniforme.
qui peut être reliée à la fonction de corrélation à 2 points des fluctuations de température sur la carte et qui est notée "Cl". Cette fonction représente l'excès de probabilité de trouver 2 surdensités thermiques
à une certaine distance par rapport à une distribution thermique uniforme.
On peut montrer que Cl=![]() où le multipôle "l" est rélié à l'échelle angulaire via la relation :
où le multipôle "l" est rélié à l'échelle angulaire via la relation : ![]()
L'analyse des données permet ensuite de dresser ce qu'on appelle le spectre de puissance angulaire du FDC:
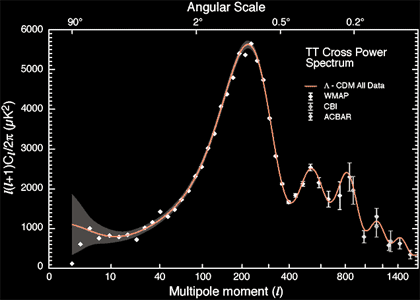
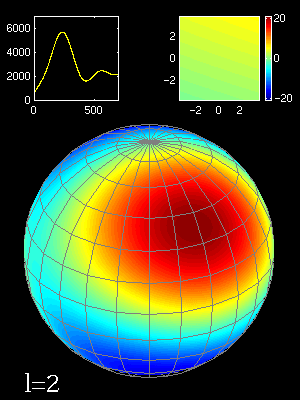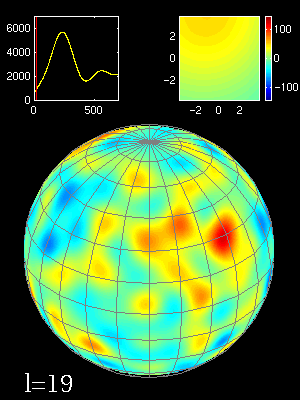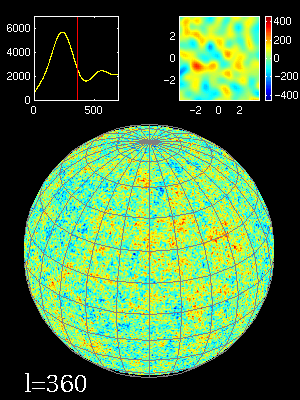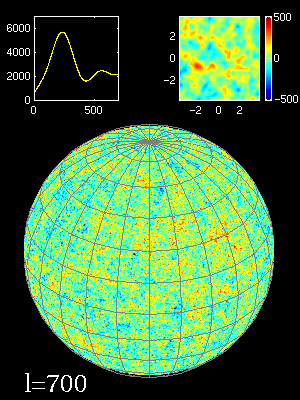
fluctuations de la T° en fonction de l'échelle angulaire
b-2-4) Pics acoustiques dans le spectre du FDC
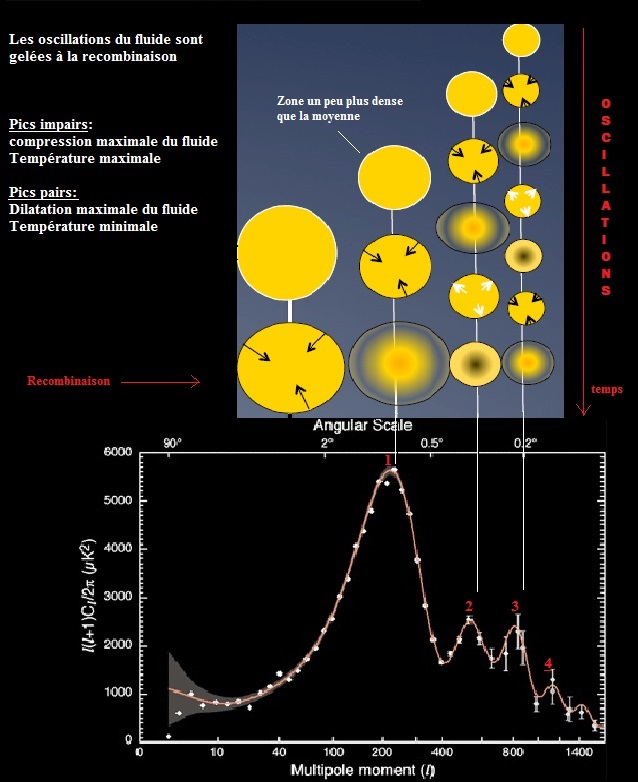
b-3) Premier pic acoustique et paramètres cosmologiques
b-3-1) Position du premier pic acoustique
Il correspond à la longueur d'onde fondamental des oscillations acoustiques au moment du découplage des photons.
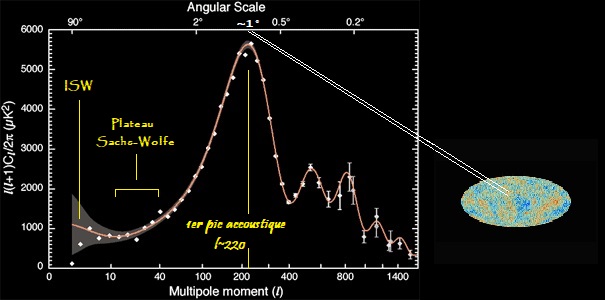

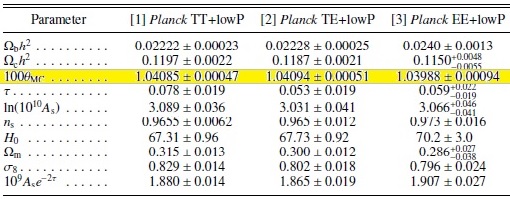
La valeur déduite des observations menées par le satelitte Planck donne 0,01041 rad. (tableau ci contre)
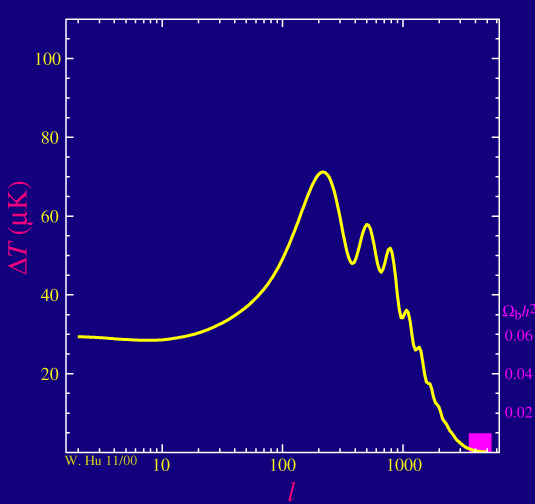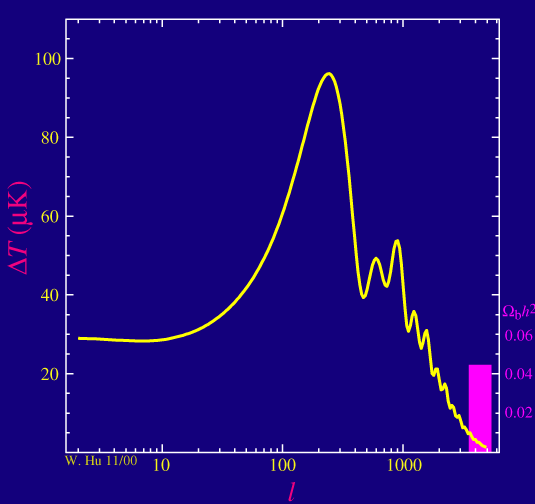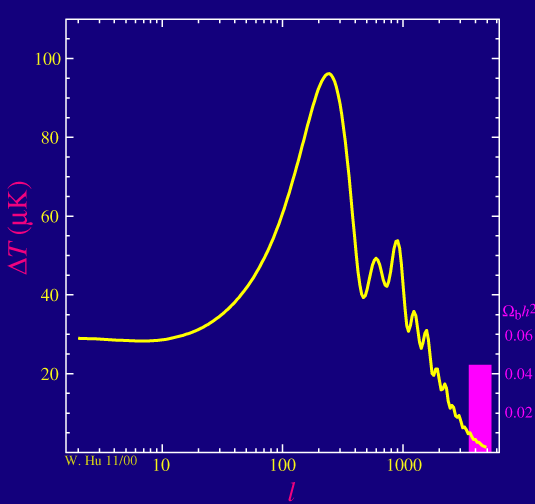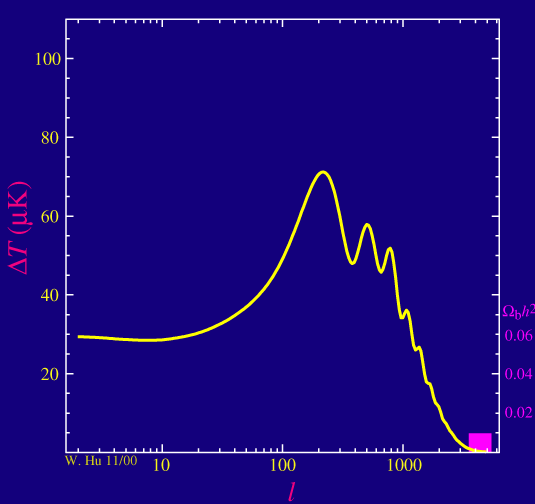
b-3-2) La densité volumique baryonique
Il est à noté que la position du premier pic dépend avant tout de la densité baryonique car celle-ci fixe la vitesse de l'onde acoustique . Une forte densité baryonique donne une vitesse du son plus faible et donc une longueur d'onde fondamentale plus importante. Le premier pic (ainsi que les autres) seront donc légèrement déplacés vers la droite ie à un multipole plus élevé. La position du premier pic teste donc avant tout les prédictions de la nucléosynthèse. Une fois la densité baryonique estimée (via la hauteur relative des différents pics), on peut dès lors évaluer la courbure de l'univers dont l'influence sur la position du premier pic acoustique est importante.
b-3-3) Le paramètre de courbure
Un des premiers paramètres cosmologiques qu'il est possiible d'évaluer grâce à la position du premier pic acoustique est la courbure spatiale de l'univers . En effet la valeur de ![]() est obtenue en divisant 2 grandeurs : La taille de l'horizon sonore
et la distance propre allant de la Terre à la surface de dernière diffusion. Malheureusement chacune de ces valeurs dépend à la fois de Ho , Wv , Wk
et Wm. Grâce à la relation Wv + Wk
+ Wm =1 , on peut néanmoins éliminer un paramètre comme par exemple Wk. La valeur de Ho est quant à
elle déduite à partir d'autres expériences comme celle utilisant les SNIA. Il reste donc 2 paramètres cosmologiques ayant un rôle sur la valeur de
est obtenue en divisant 2 grandeurs : La taille de l'horizon sonore
et la distance propre allant de la Terre à la surface de dernière diffusion. Malheureusement chacune de ces valeurs dépend à la fois de Ho , Wv , Wk
et Wm. Grâce à la relation Wv + Wk
+ Wm =1 , on peut néanmoins éliminer un paramètre comme par exemple Wk. La valeur de Ho est quant à
elle déduite à partir d'autres expériences comme celle utilisant les SNIA. Il reste donc 2 paramètres cosmologiques ayant un rôle sur la valeur de ![]() : Wv et Wm et dont la somme est notée WT = Wv + Wm = 1 - Wk
: Wv et Wm et dont la somme est notée WT = Wv + Wm = 1 - Wk
En jouant conjointement sur les deux valeurs Wv et Wm, on essaie de reprodruire à l'aide d'un logiciel la courbe du spectre en puissance du FDC obtenue via Planck. Le meilleur ajustement donne une valeur de WT = 1,02 (+- 0,02) d'où l'on déduit que Wk est très proche de 0. La courbure spatiale de l'univers semble donc nulle aux incertitudes près.
Plus généralement une valeur de Wk <0 (univert fermé) donnerait une valeur de ![]() plus grande c'est à dire une valeur beaucoup plus faible pour le multipôle correspondant au premier pic acoustique et inversement si l'univert est spatialement ouvert.
plus grande c'est à dire une valeur beaucoup plus faible pour le multipôle correspondant au premier pic acoustique et inversement si l'univert est spatialement ouvert.
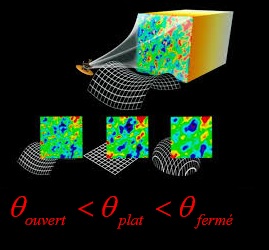
Sur l'animation ci-dessous, les 2 variables qui ont été choisit sont Wv et Wk que l'on fait varier conjointement via le paramètre 1-Wm =Wv + Wk
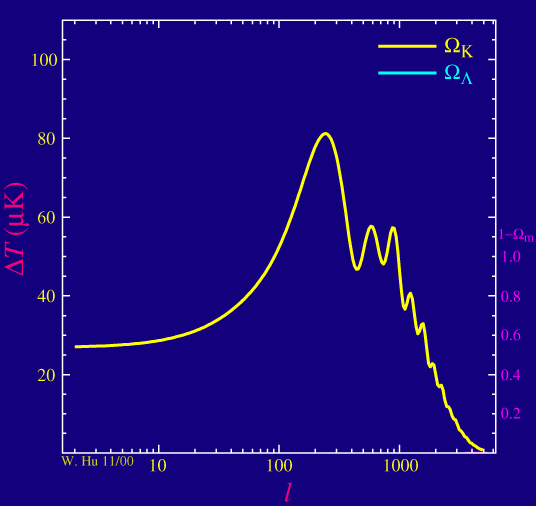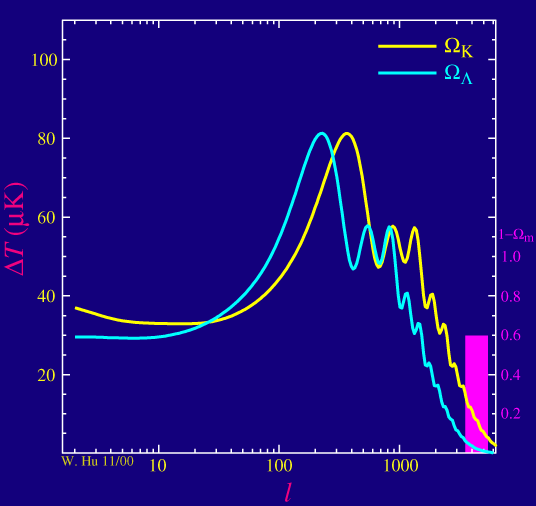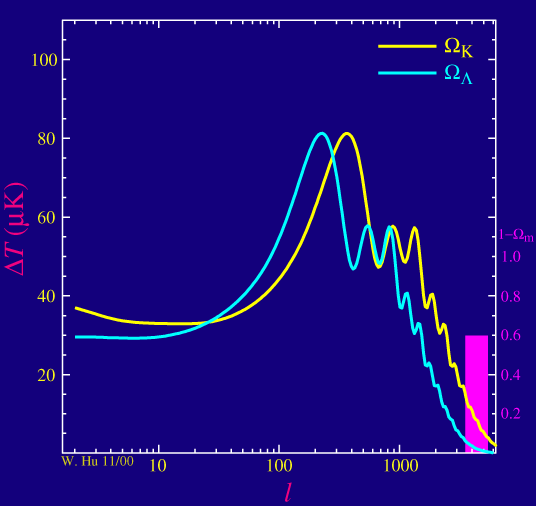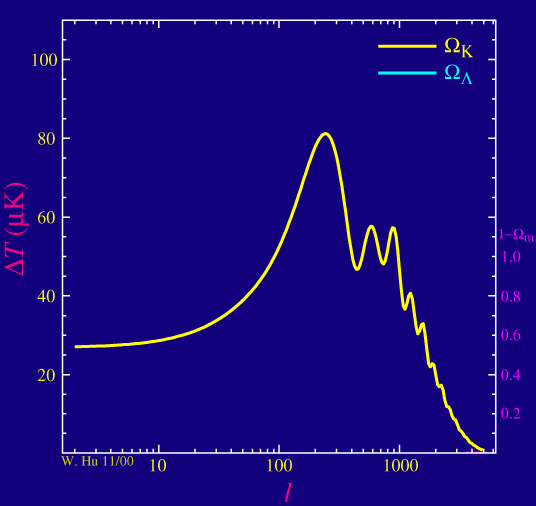
Faire varier les paramètres cosmologiques et visualiser le spectre en puissance angulaire du FDC : https://lambda.gsfc.nasa.gov/toolbox/tb_camb_form.cfm
